Acknowledgements - Hench_et_al_CSR

Discussion and conclusions cont'd

Appendix A. Rotation of momentum equations into a streamwise-normal coordinate system

Hench_et_al_CSR_02
Page Navigation
14

J.L. Hench et al. / Continental Shelf Research 22 (2002) 26152631

2628

for inlets based on a dynamical analysis. The four

idealized inlets analyzed here provide baseline

qy |ffl{zffl}

|{z} |fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl} M

cases for the dynamics one might expect at natural

My1

My2

inlets.

pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi!

Cf U 2 V 2

V 0:

A:2

|fflffl{zfflffl} |fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}

Acknowledgements

My4

My5

We thank two anonymous reviewers for con-

For simplicity, horizontal diffusion terms are

structive comments that significantly improved the

omitted from (A.1) and (A.2) as they did not

manuscript. Funding for this study was provided

contribute significantly to the momentum balances

by the Coastal Inlets Research Program (CIRP) of

of our inlet simulations. At each time-step, we

the Coastal Hydraulics Laboratory, US Army

define a two-dimensional, orthogonal, curvilinear

Corps of Engineers, and the Naval Research

coordinate system such that at each grid point, one

Laboratory, Office of Naval Research (award

coordinate direction points in the along-stream

N00014-97-C-6010).

direction s and the other points in the across-

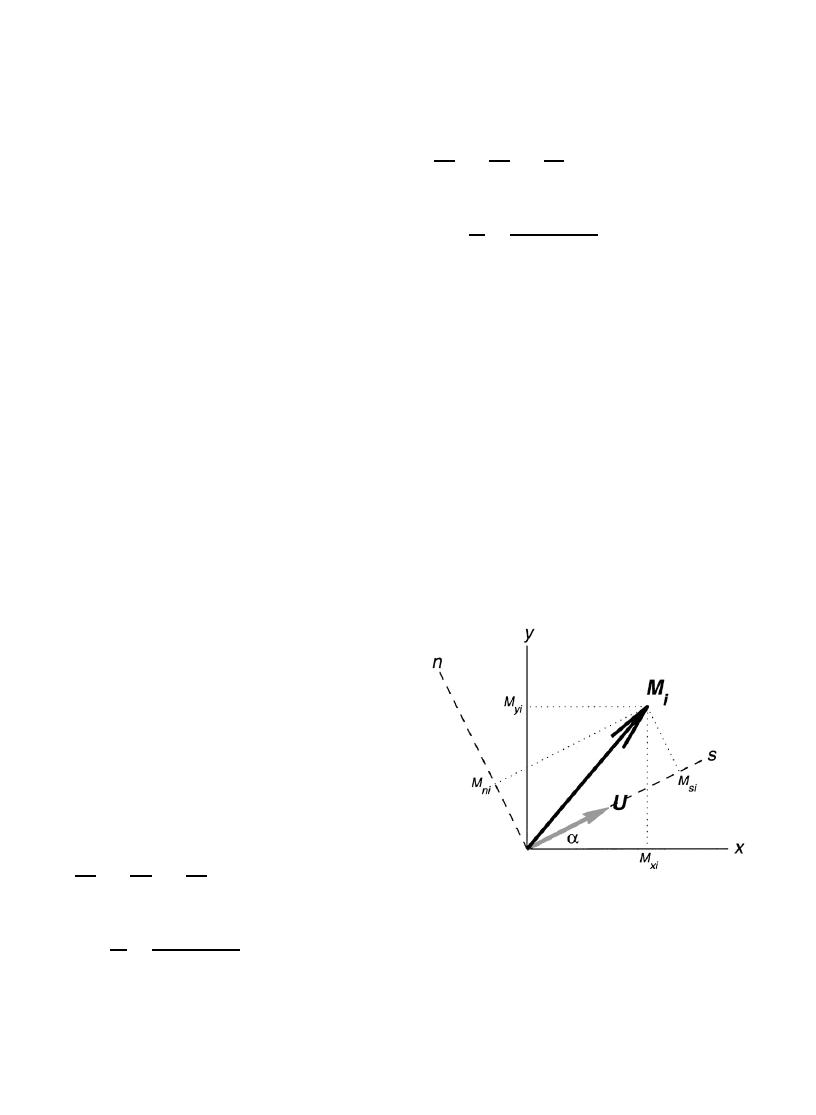
stream direction n in the right hand sense (see

Fig. 8). The orientation of the s2n coordinate

Appendix A. Rotation of momentum equations into

system relative to the original fixed x2y coordi-

a streamwise-normal coordinate system

nate system, as expressed by the streamline angle

ax; y; t; varies such that at all points the along-

The use of a streamwise-normal coordinate

stream velocity Us is equivalent to the speed, and

system allows a more intuitive physical interpreta-

the across-stream velocity Un 0: From Fig. 8, it

tion for strongly curving flow fields. Gill (1982)

should be apparent that momentum terms in s2n

elegantly derives the steady frictionless form of the

two-dimensional momentum equations directly in

the s2n coordinate system. Here we derive

corresponding transient frictional equations by

transforming the familiar x2y equations. This

transformation is useful in that standard x2y

momentum terms can be used to directly compute

term values in the s2n coordinate system. The

procedure is as follows. U x; y; t; V x; y; t and

Zx; y; t are computed on a fixed x2y grid for all

time steps. The elevation and velocity fields are

used to reconstruct each term in the x2y

momentum equations at each node in the x2y

grid. We designate the individual x2y momentum

terms Mxi and Myi as

qy |ffl{zffl}

qz}

Fig. 8. Definition sketch for the streamline coordinate system.

|{ |fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl} M

At each computational node a s2n coordinate system is

Mx1

Mx2

established and aligned with the local velocity vector U : The

pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi!

local axes rotation angle is ax; y; t: Mi represents the ith force

Cf U 2 V 2

or acceleration vector in the momentum equations, with x2y

U 0;

A:1

qfflx

components Mxi and Myi (e.g. g qZ=qx and g qZ=qy). Mi is

|fflffl{zffl }

|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}

rotated on to the s2n axes to determine local streamwise and

Mx4

Mx5

normal components Msi and Mni (e.g. g qZ=qs and g qZ=qn).

Index

Privacy Statement
Press Release
Contact