1070
S.A. Hughes / Coastal Engineering 51 (2004) 10671084
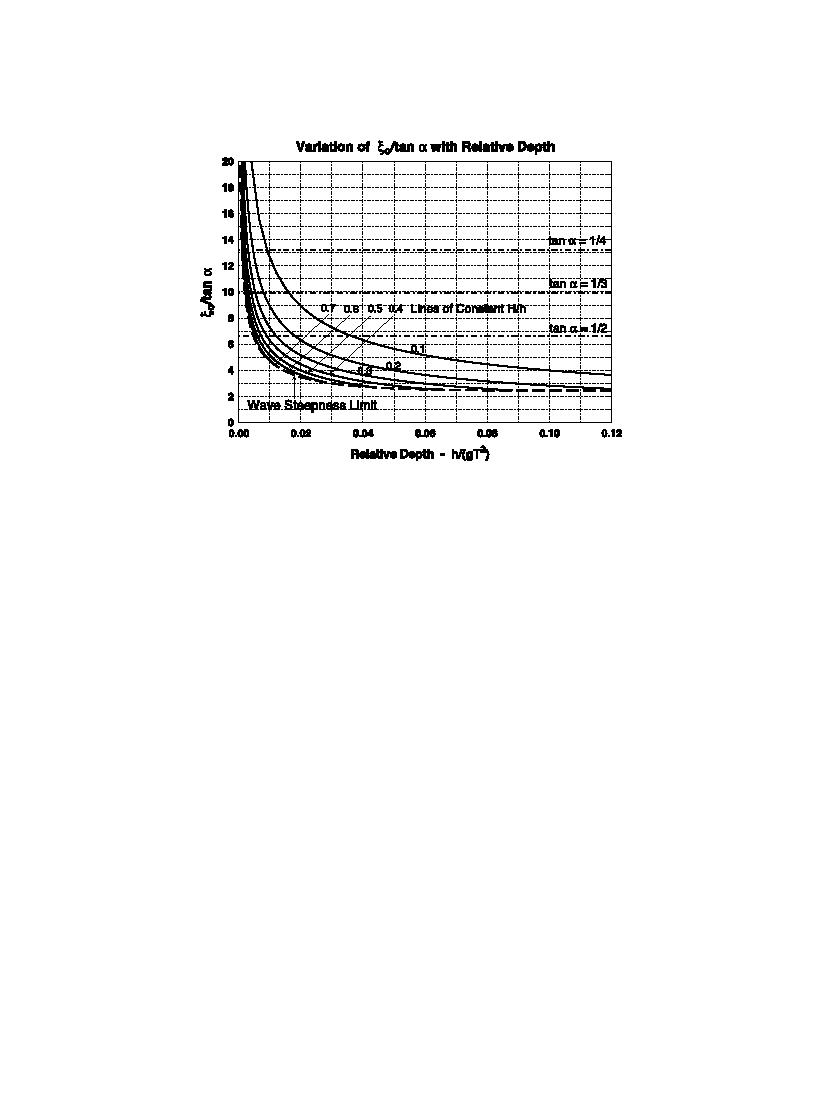
Fig. 1. Variation of (H/Lo)1/2 with h/gT2 for constant values of H/h.
limit as defined by Williams (1985) and expressed
surf zone processes due to plunging and spilling wave
by Sobey (1998) as a rational function. The
breaking.
horizontal chain-dashed lines represent the demarca-
tion (no=3.3) between surging/collapsing breakers
(above the line) and plunging/ spilling breakers
3. Criteria for a new wave parameter
(below the line) for different slopes. Similar trends
arise if H/Lo is replaced with local wave steepness
Partial motivation for developing a new wave
H/L.
parameter for nearshore coastal processes and coastal
structure design comes from the Hudson armor
same value of deepwater wave steepness. In partic-
stability equation and other stability equations based
on the armor stability parameter, H/DDn50. Examina-
ular, a wave in shallow water having the same height
and period as a wave in deeper water will have the
tion of Hudson's (1959) development of the stability
same deepwater wave steepness, but different wave
equation reveals that wave height enters the armor
kinematics. The wave in deeper water will behave
stability parameter as a near-breaking long-wave
more like a linear wave whereas the wave in shallow
approximation of horizontal water velociffitffiyffiffi in the
p ffiffi
water will exhibit more nonlinearity. Furthermore, a
vicinity of the still water level, i.e., Vw~ gH . From
change in wave height occurs as the deeper water
a physical perspective, this seems to be a gross
wave moves into shallow water, so it is possible that
simplification of wave effects on armor stability.
by the time the deeper water waves reaches the depth
However, because of other complexities related to
of the shallow water wave, the wave height will be
armor stability (randomness of armor matrix, armor
different. Thus, deepwater Iribarren number based on
support points, interlocking, etc.), the lack of a more
local wave height may not be the best parameter for
rigorous description for wave loading may not have
correlations involving waves prior to breaking, or for
been too detrimental. Most established stability
waves described as surging or collapsing breakers,
coefficients for use with the Hudson equation were
because the influence of water depth is not included.
based on the more conservative observations rather
However, ample evidence supports the use of deep-
than the mean of the data. Nevertheless, there remains
water wave steepness H/Lo (and no) for correlations to
the possibility that the observed scatter in armor





 Previous Page
Previous Page
