E2
E3
E1
En
zj
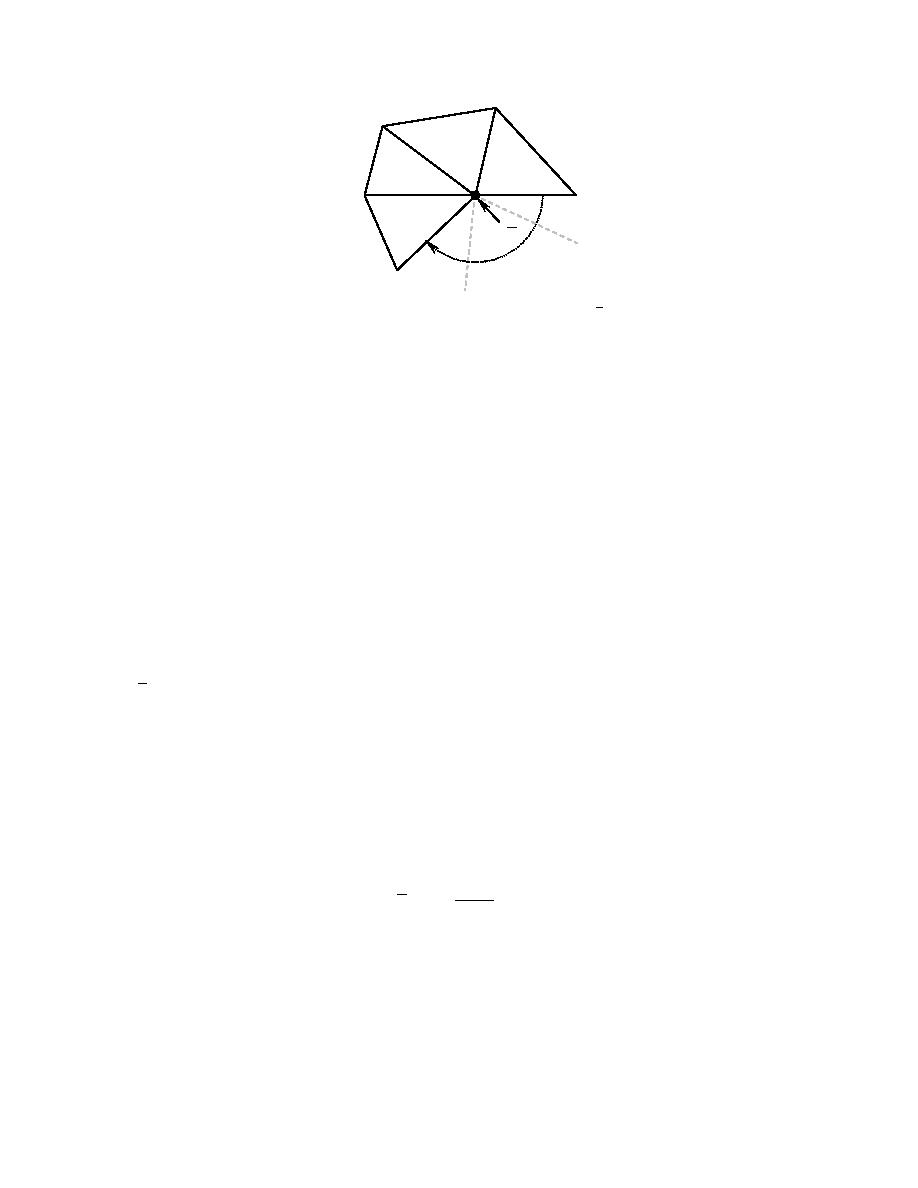
Fig. 4:
Node j surrounded by n elements; the continuous approximation z j for node j is determined
from the (possibly) n unique values from the elements surrounding the node.
3.5
Continuous projection procedure
As previously mentioned, ADCIRC makes use of approximations that are continuous in
space across the entire domain. Thus, in addition to our discontinuous approximation zh, we must
also compute a continuous approximation which must be fed back into ADCIRC after computing
the updated bathymetry. We wish to accomplish the following with our procedure: given a node
j which is a vertex for n different elements we wish to compute a single nodal value denoted by
z j based on the n (possibly) unique values at that node that are obtained from the DG method
within the individual elements attached to that node (see Fig. 4). We have experimented with
several different approaches for obtaining these single nodal values and based on numerical
experiments have implemented an angle based weighted average given by:
⎛ ∠i
⎞
n
z j = ∑⎜
(24)
zvi ⎟
i=1 ⎝ ∠SUM
⎠
where ∠i is the angle of the vertex of element i and ∠SUM is the total sum of the vertex angles
around node j. We have also experimented with weighted area averaging and centroidal type
18





 Previous Page
Previous Page
