COASTAL ENGINEERING 2004
2625
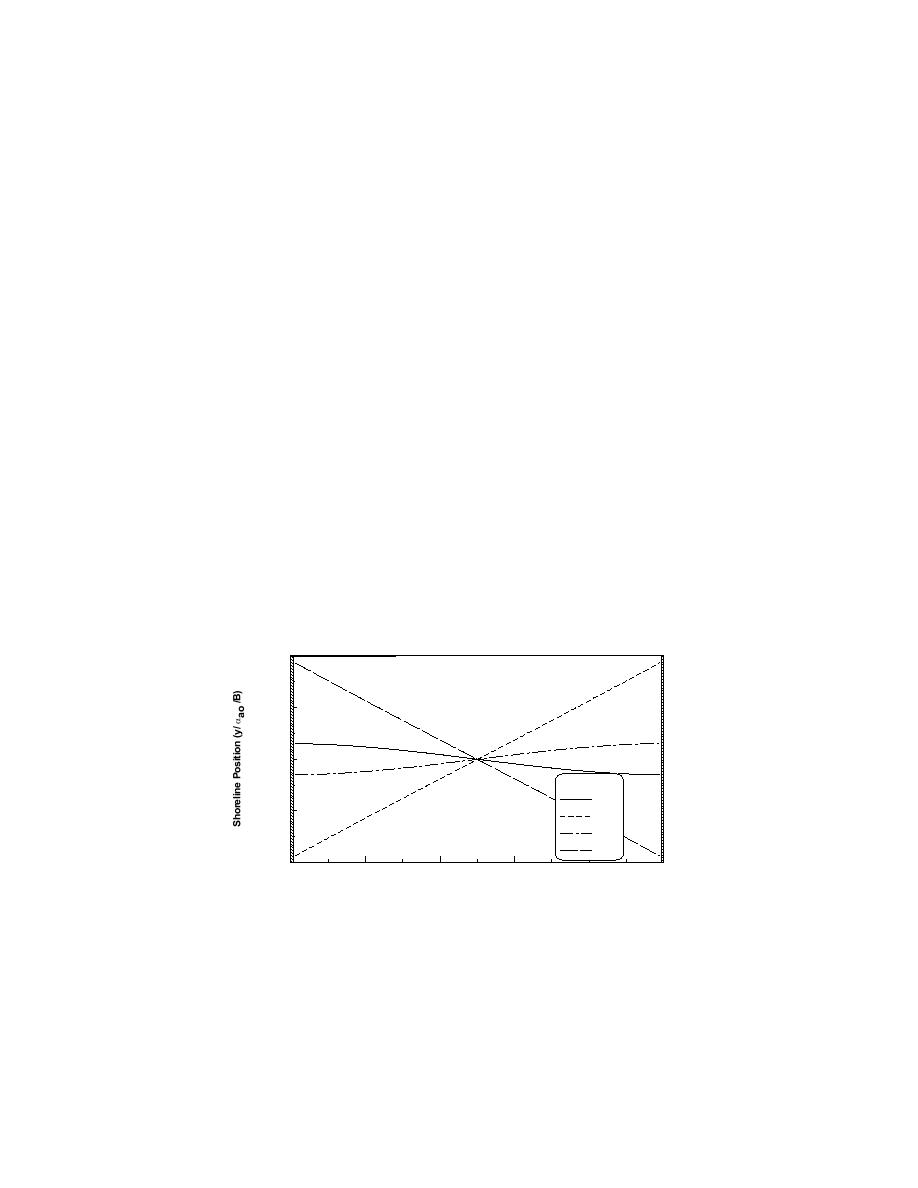
response in shoreline orientation to the incident waves, and the shoreline lies
almost parallel to the wave crests at all times (Fig. 2). The parameter ζ becomes
small if the amplitude of the transport rate Qo is large, the length of the enclosed
beach B small, or the frequency ω of the wave angle variation small. For large ζ
there is a distinct phase difference between the shoreline response and αo (Fig.
3) and the oscillation in the shoreline position is less than for smaller ζ For very
large ζ, there will be no effect on the shoreline except close to the boundaries.
The complete solution also has a transient part. However, this part decays
exponentially with time and is not included in (11).
4.
Analytic Solution of Shoreline Change at a Single Groin including
Offshore Losses in a Rip Current
As indicated by the previous case, situations with higher values on the
morphodynamic response factor ζ result in shorelines with larger curvature
( ∂2 y / dx2 ) near the groin. Thus, with the shoreline orientation closest to the
groin corresponding to Q = 0 as well as a zero wave-generated longshore
current, a larger curvature indicates that the shoreline orientation a bit further
away from the groin corresponds to a larger transport rate (and longshore current
velocity) that, if directed towards the groin, is anticipated to generate an offshore
rip-related transport. This also follows from Eq. (6) where Q is seen to be
proportional to ∂y/∂x, leading to ∂Q/∂x ~ ∂2y/∂x2. In mathematical terms this
boundary condition at the groin location is formulated as,
0.50
0.25
0.00
Phase
0
-0.25
π/2
π
3π/2
ξ=1
-0.50
0.0
0.2
0.4
0.6
0.8
1.0
Alongshore Distance (x/B)
Figure 2. Shoreline evolution in enclosed groin compartment at steady-state conditions when
breaking-wave angle varies sinusoidally with time for ζ = 1. (Modified from Larson et al. 1997).





 Previous Page
Previous Page
