2628
COASTAL ENGINEERING 2004
1.0
0.8
0.6
0.4
0.2
0.0
0
2
4
6
8
10
Elapsed Dimensionless Time (ε t/ L2 )
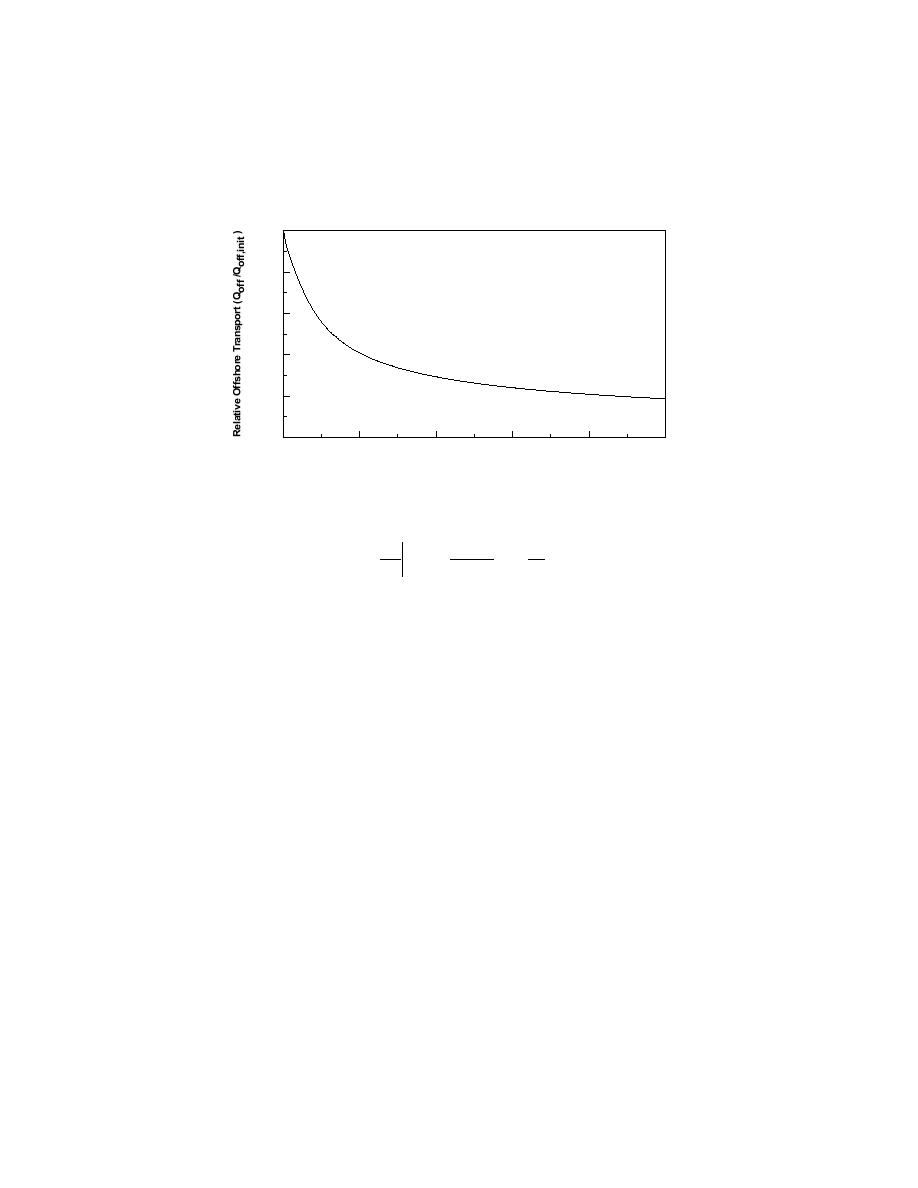
Figure 5. Relative offshore transport rate as a function of elapsed dimensionless time.
problem numerically the offshore rip loss is expressed in a slightly different way
(formulated here for the loss Qoff,L at the left-hand lateral boundary),
Q - Q1
ΔQ
Q
Qoff ,L = - R
= -R 2
= -R 2
(16)
Δx i=1
Δx
Δx
where x is the alongshore grid spacing and Q1 is the transport across the lateral
boundary. With an impermeable, long groin located here, the boundary
condition is formulated Q1 = 0. An equivalent boundary condition is formulated
for the right-hand boundary. Figure 6 illustrates simulated interrelations
between the offshore losses at each of the two groins (where Qoff,R is the loss at
the right-hand lateral boundary) for a situation where the incident wave angle
flips instantaneously between 11.5 and 11.5 deg every two months. The
simulation starts out with a negative angle inducing an offshore rip current and
associated offshore losses at the left-hand groin. The offshore transport rate
starts out with a high value but decreases quite rapidly (in about two weeks) to a
considerably lower value that remains fairly stable in time at around 5 m3/h.
Simultaneously, the shoreline adjacent to the left-hand groin progrades towards
the groin tip as it recedes at the right-hand groin. Because the initial shoreline
was located at x = 0, the system is somewhat asymmetrical initially while at the
end of the third cycles it seems like symmetry has been reached.
A series of simulations was then run to illustrate the impact of the
morphodynamic response factor ζ on the offshore rip losses following the above
formulation of the lateral boundary conditions. In all cases, the wave angle
varied sinusoidally according to Eq. (10) with 1/ set to 1, 2.25, 4, 9, and 36
days, respectively. With constant wave period T = 3 sec, breaking wave height





 Previous Page
Previous Page
