|
|
|
102
Rodney J. Sobey
Lateral structure of uniform flow
Journal of Hydroinformatics
06.2
2004
|
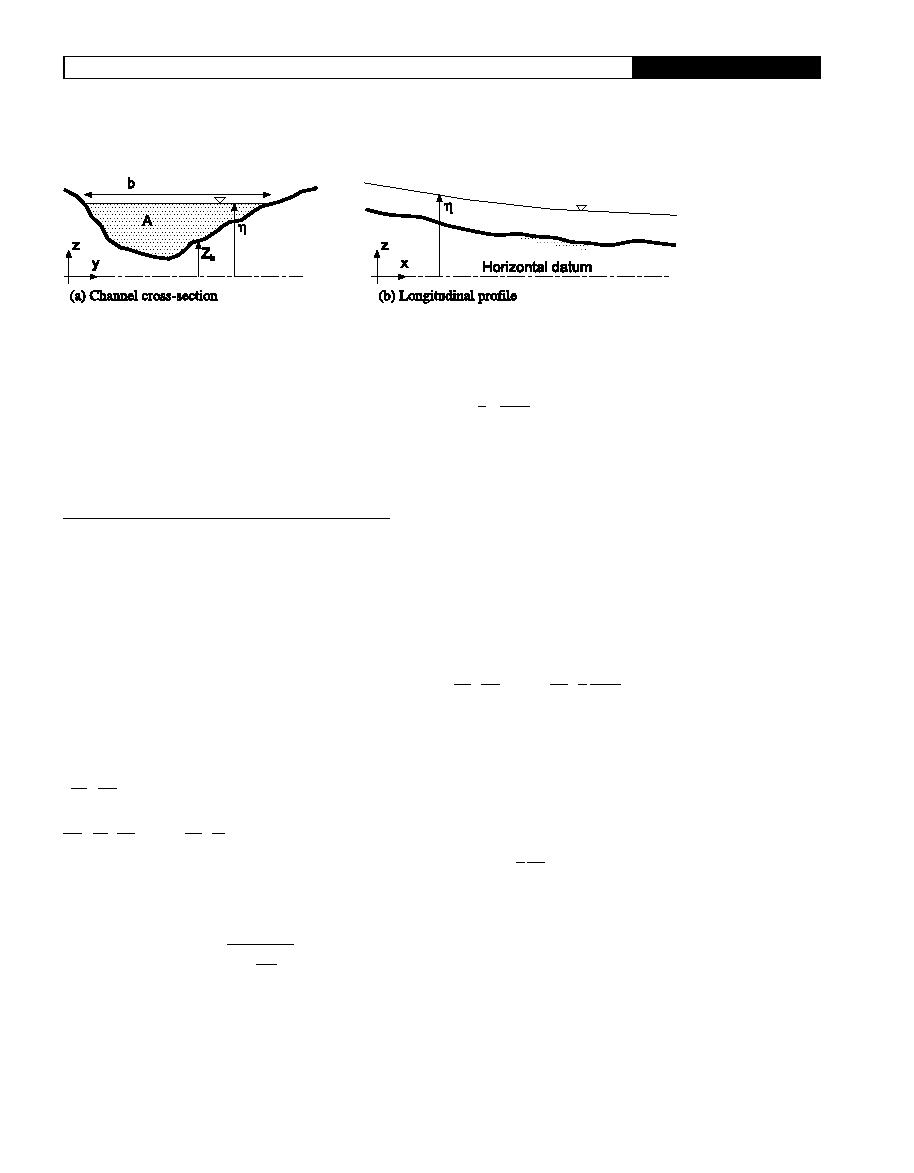
Figure 1
Definition sketch for narrow channel.
viscosity. Illustrative predictions are provided for a
zQzQ
t0 f r
(3)
rectangular and a natural channel.
A2
8
in which f is the DarcyWeisbach friction factor. The
alternative Chezy or Manning models can be substituted
`
without any fundamental change in the analysis. These
details are given subsequently.
CROSS-SECTION-INTEGRATED DESCRIPTION
The special case of steady flow has received consider-
able attention in open channel flow. Omitting the time-
Most analyses of nearly horizontal flow in natural
dependent terms, the long wave equations reduce to the
channels adopt a cross-section-integrated description
gradually varied flow equations:
(see Figure 1). The independent variables are longitudinal
position x and time t, the dependent variables are h(x,t)
the local water surface elevation to a fixed horizontal
Q constant
SD
datum and Q(x,t) the local discharge or cross-section-
Q2
dh f uQuQ
d
52gA
P
(4)
2
integrated flow.
dx 8 A2
dx
A
The cross-section-integrated conservation equations
are
which describe the steady-state flow on which flood and
tidal flows are imposed (Henderson 1966). For uniform
Q
∂h
flow, dA/dx is zero, so that dh/dx ( = dzb/dx = - S0), A
∂
0
b
∂t ∂x
and P are also constant, and
SD
Q2
∂Q
∂h
0
gA
∂
t P
(1)
∂t
∂x
A
∂x r
Q2
0 gAS0 f 2 P.
(5)
8A
in which A(x,t) is the local flow cross section, P(x,t) is the
local wetted perimeter,
For a flat-bottom channel (rectangular, trapezoidal, etc), a
uniform (h - zb)n = dn depth (the normal depth) can be
OE
D
2
dzb
established by solution of implicit algebraic Equation (5).
*
1 S
A * h zb dy, P
(2)
dy
dy
But note that this requires the additional assumption that
Bed
A
the lateral water surface profile is horizontal.
zb(x,y) is the local bed elevation, b(x,t) is the local surface
For a natural channel, the depth varies across the
channel and the concept of a normal depth is not
boundary shear. The quadratic DarcyWeisbach friction
especially satisfactory. But the concept of uniform flow
model is adopted, with
remains appropriate. It would be more useful to



 Previous Page
Previous Page
