R.J. Sobey, S.A. Hughes r Coastal Engineering 36 (1999) 1736
29
would be about 7 s observational points in a half-window. For J s 3 and s s 1, there
would be 14 unknowns and 35 equations. For J s 3 and s s 4, there would be 35
unknowns and 140 equations. With initial estimates provided by a global Airy theory
approximation, smooth and robust solutions are established in each extra-wide half-
window. These in turn provide routinely appropriate initial estimates for the local
solutions in very much narrower windows.
The algorithm had most difficulty in finding credible local solutions around the
zero-crossings of the P trace. At such regions, profile curvature is very small and a
narrow local window has poor resolution. Often, this is not a region of particular
concern. Two strategies are possible in dealing with this problem. The first would be to
ignore such points and rely on interpolating for the kinematics from adjacent local
solutions that bracket the zero-crossings. The second would be to extend the local
window to improve resolution of the local profile curvature. This second approach has
been adopted, and was the essential rationale for the double-width window introduced
above.
6. Theoretical wave traces
An initial evaluation of the LFI-PUV theory and coding is provided by theoretical
PUV traces from uniform, long-crested wave trains. Three monochromatic waves,
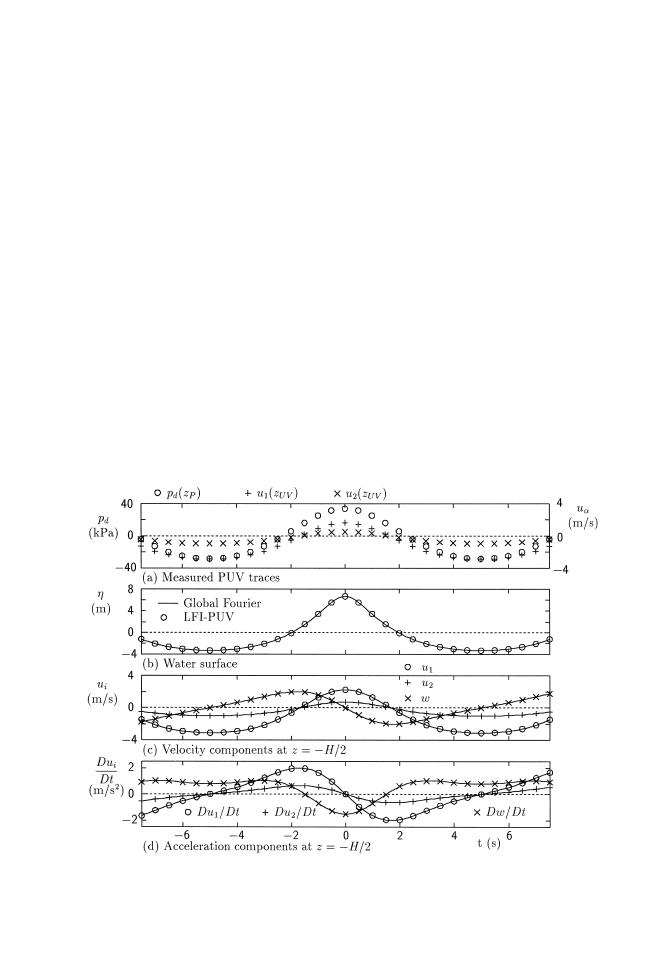
Fig. 4. LFI-PUVw3,3,0.1x predictions for wave `Twenty'.





 Previous Page
Previous Page
