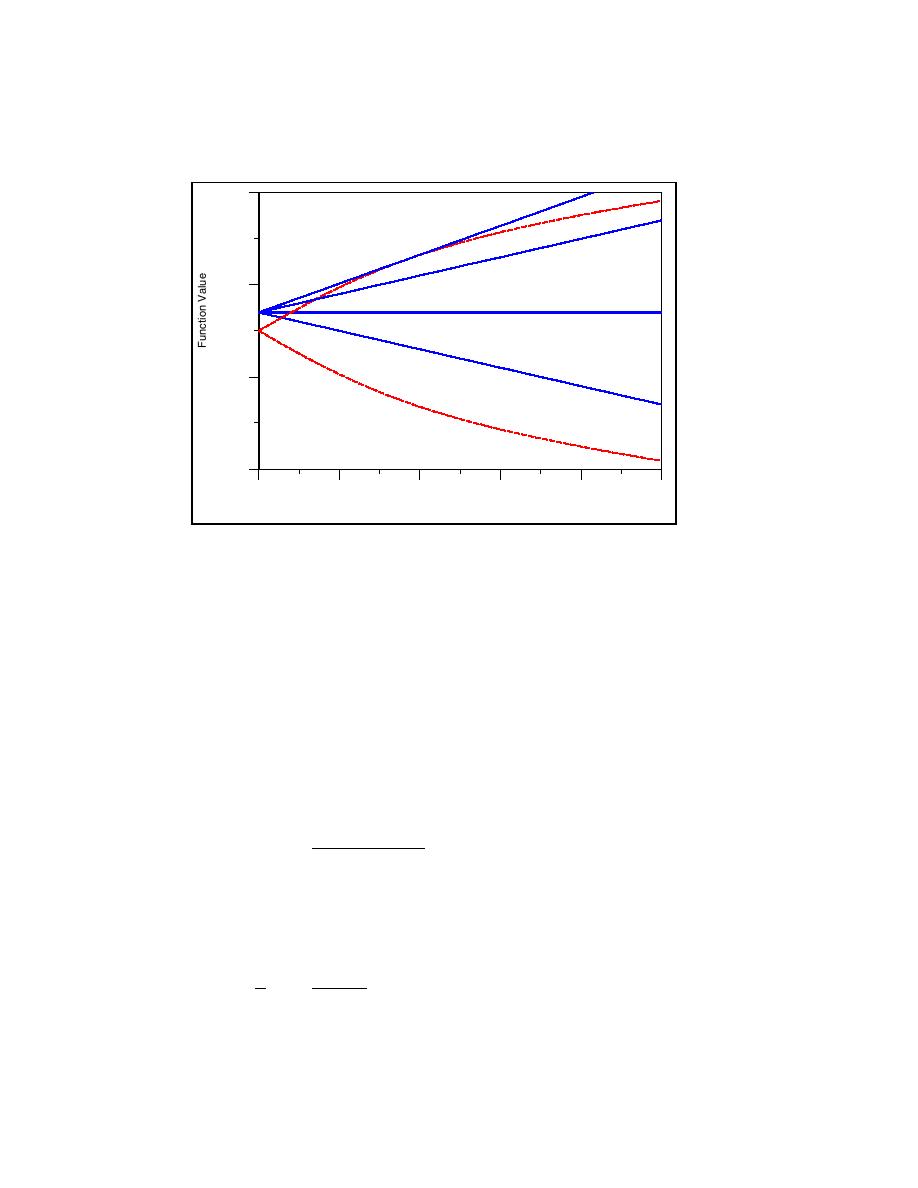
following current produces an increase in L, and an opposing current a
decrease in L in comparison to the case of no current (all other factors held
constant).
0.75
Blocking current
Opposing current
E
0.25
A
No current
D
C
B
Following current
-0.25
-0.75
0.0
0.1
0.2
0.3
0.4
0.5
Relative Water Depth, d/L
Figure 2. Examples of solutions to dispersion equation with current present
(after Jonsson 1990)
Wave Orthogonals and Wave Rays
In the presence of a current, the wave energy will not be conserved along
the wave orthogonals, instead the energy is conserved along the wave rays
that have the absolute group speed Cga as a tangent at all locations. The wave
ray direction β depends of the relative wave group speed and the current
considerations (Jonsson 1990; also, see Figure 1) to yield:
Cga = (Cgr + U 2 + 2CgrU cos(δ - α) )
1/ 2
2
(8)
U sin(δ - α)
β = α + arctan
(9)
U cos(δ - α) + Cgr
where Cgr is the relative group speed and α the direction of the wave
orthogonal. The relative group speed is determined from linear wave theory
according to:
1
2kd
Cgr = Cr 1 +
(10)
2 sinh 2kd
From Equation 9, it may be concluded that if U cos(δ-α) = -Cgr, the
denominator is zero, and the wave rays form a 90-deg angle with respect to
14
Chapter 3 Wave Model





 Previous Page
Previous Page
