3000
2000
1000
60
50
70
0
Pole
Log Spiral
-1000
-7000
-6000
-5000
-4000
-3000
-2000
-1000
0
1000
Distance Alongshore, m
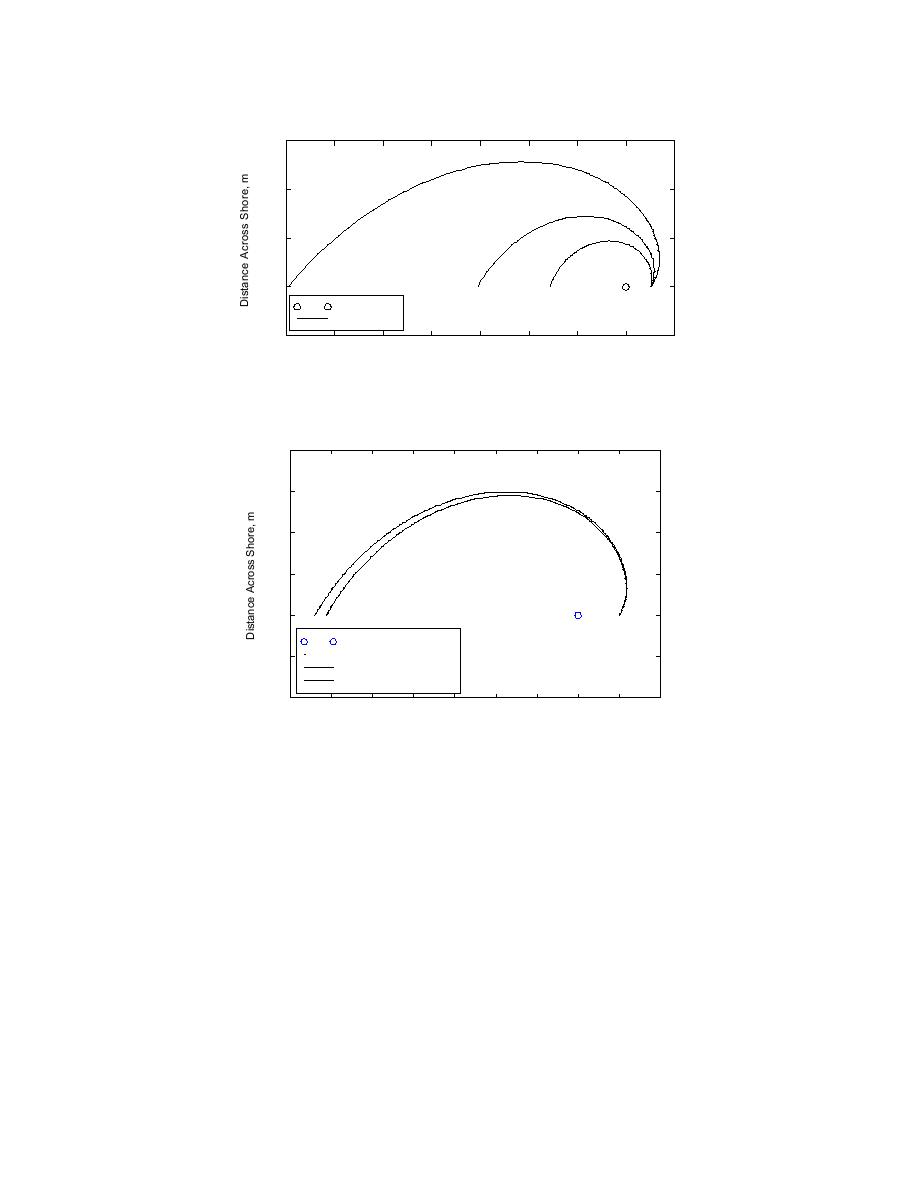
Fig. 2. Variation of logarithmic-spiral shape with α (R0 = 500 m).
2000
1500
1000
500
0
Pole
Log-spiral α = 60.6
-500
Log-spiral α = 60.0
Log-spiral α = 59.4
-1000
-3500
-3000
-2500
-2000 -1500 -1000 -500
0
500
1000
Distance Alongshore, m
Fig. 3. Sensitivity of log-spiral shape to small variations of the parameter α (R0 = 500 m).
To analyze the validity of the assumption that headland-bay beaches can be
adequately described by a log-spiral function, the pole location, radius at origin of angle
measurement (scaling factor), and the spiral characteristic angle α must be identified,
giving four unknowns. If the pole position is known, a solution procedure for the best-fit
shape, that is, to find the best-fit value of α, follows. Eq. 1 can be rewritten as
ln (R) = ln (R0 ) + θ cot α
(2)
where R = radius to point P, θ = angle between polar axis and radius vector to point P.
This linear relationship is convenient for fitting a log-spiral curve to data. The slope of
the straight line is cot α, from which α can be obtained.
A computer program was written that searches for the pole position while minimizing
the fitting error. It also determines the characteristic angle α that best fits the shoreline
Moreno & Kraus
5





 Previous Page
Previous Page
