W = w sin(σt)
x
η
t=0
h
h
L
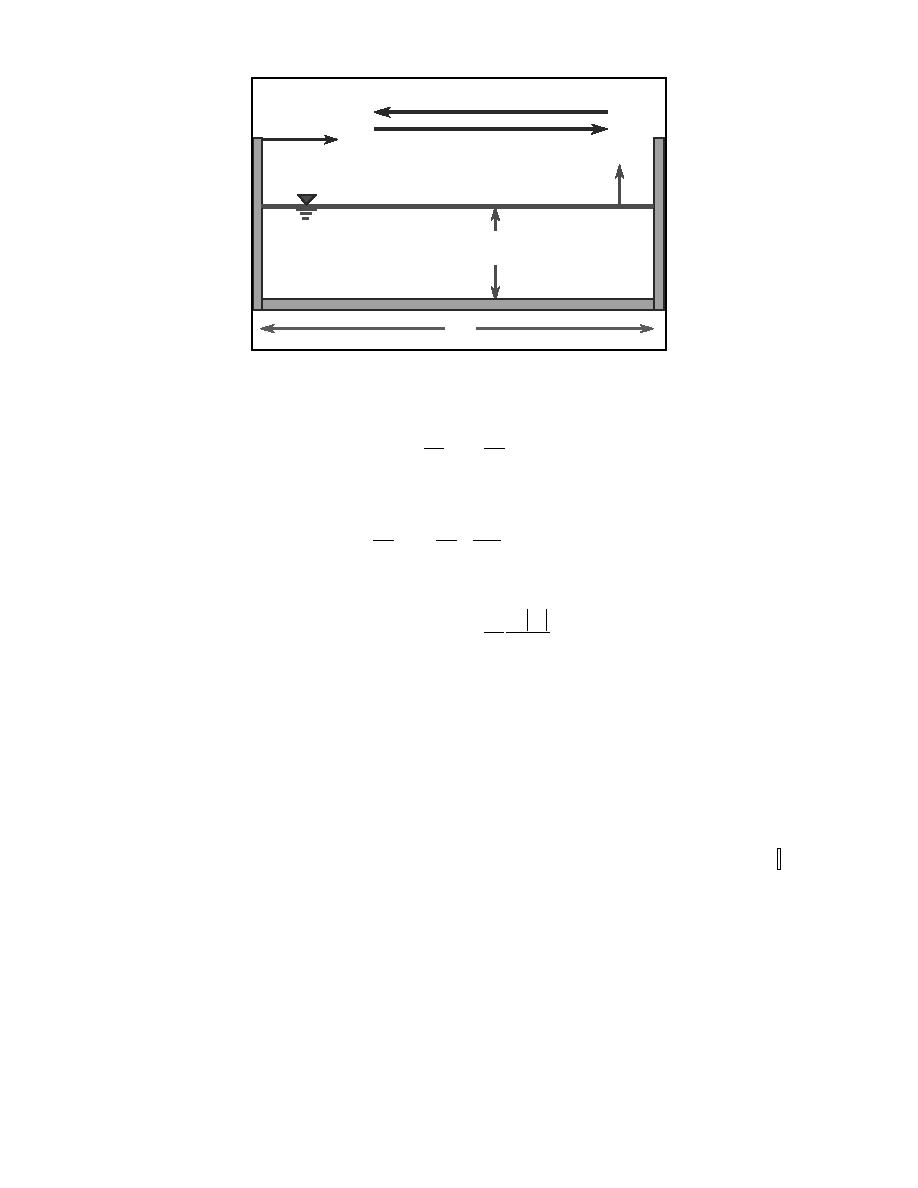
Fig. 1. Sketch of one-dimensional basin with wind forcing, t =0
The continuity and momentum equations (Eqs. 5 and 6) then become
∂η
∂u
= -h
(7)
∂t
∂x
and
∂η C fL
∂u
= -g -
u+F
(8)
∂t
∂x
h
where the wind forcing is represented by the function
ρa W W
F = F (t ) = CD
(9)
ρ h
for pure oscillatory wind specified by Eq. 1 with w0 = 0. Although the wind-drag
coefficient varies with the wind speed in some formulations, it is taken to be constant for
this derivation, as is CfL.
From Lamb (1945), Ippen and Harleman (1966), and others, linear equation systems
such as Eqs. 7 and 8 can be solved by differentiating Eq. 7 with respect to x and Eq. 8 with
respect to t, then adding the resultant equations to eliminate η. The one-dimensional
inhomogeneous wave equation for u is obtained,
utt + 2d ut - c2uxx = Ft
(10)
in which notation was simplified by defining d = CfL/(2h), and where c2 = gh. The
subscripts denote partial differentiation with respect to t and x. The quantity d has the
with the depth.
For the idealized basin, the initial and boundary conditions on u are, respectively,
u(x, 0) = ut(x, 0) = 0, and u(0, t) = u(L, t) =0. The water surface is specified to be initially
horizontal, and the wind begins blowing at t = 0. Symmetry indicates that the problem can
be solved over half the basin, for example, on [0, L/2]. In the solution procedure that
4
Kraus & Militello




 Previous Page
Previous Page
