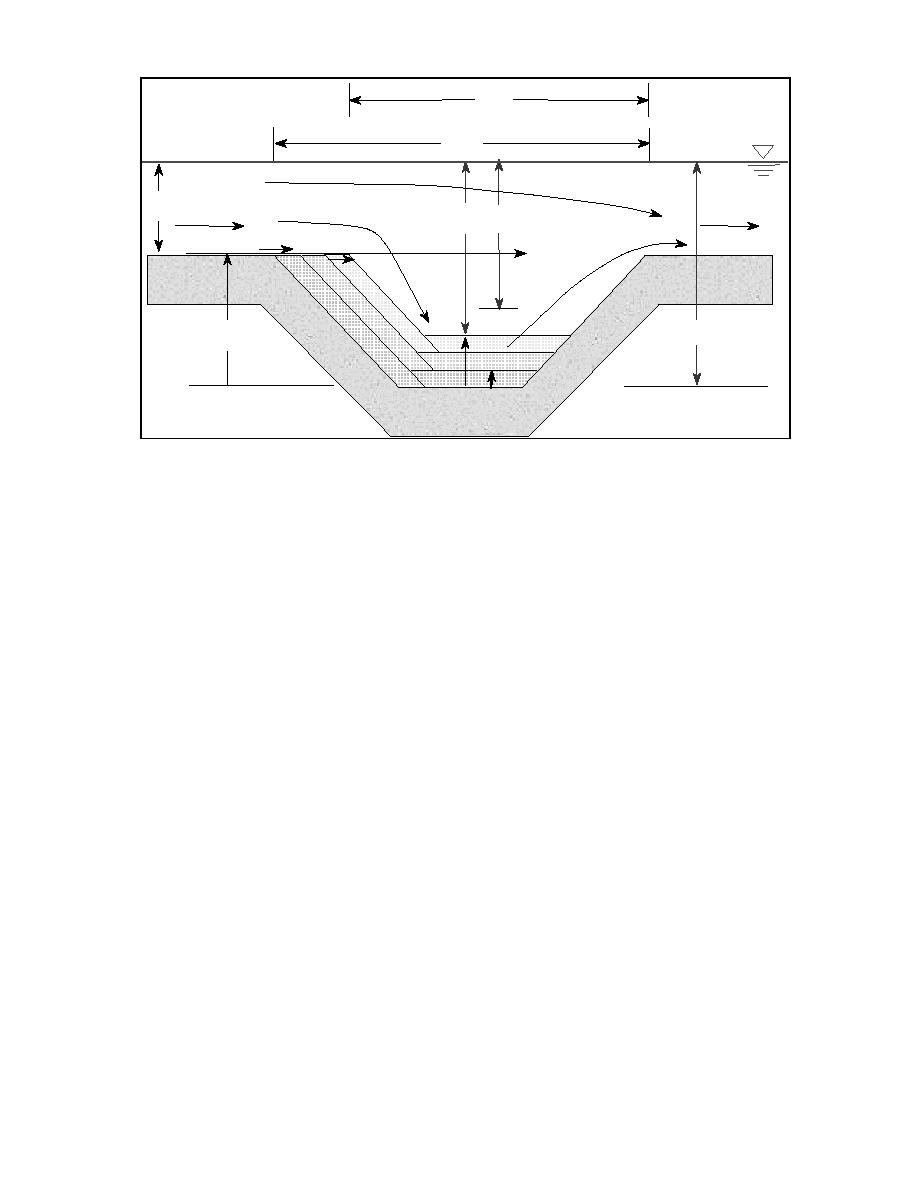
W
W0
qs
ha
qd
q
qy
hp
h
qb
∆x
x
qr
h0
z0
z
∆z
Fig. 2. Definition sketch for channel infilling model
The transport rate q per unit length of channel near the updrift side of the channel can be
divided into a bedload transport rate qb, a rate of suspended material deposited into the
channel qd , and a rate qs of suspended material passing over the channel. For the situation
of a coastal inlet, for the portion of channel crossing the surf zone, the transport rate per
unit channel length can be estimated as the total transport rate Q multiplied by the ratio of
length of channel exposed to the longshore transport to the total width of the surf zone.
From Fig. 2 and above discussion, the transport rate per unit length of channel is
represented as:
q = qb + qd + qs
(2)
The rate qc of material filling the channel is the sum of that entering and that resuspended
and leaving the channel:
qc = qb + qd - qr
(3)
The rate qy of material bypassing the channel is given by the sum of qs and the rate qr of
material resuspended from the channel:
qy = qs + qr
(4)
It is seen that q = qc + qy (= qb + qd + qs ) .
A closure assumption of the model is that the rate of material resuspended from the
channel bottom is proportional to the product of the depth of the channel (normalized by
the total channel depth) and the rate of deposition as,
Kraus and Larson
4




 Previous Page
Previous Page
