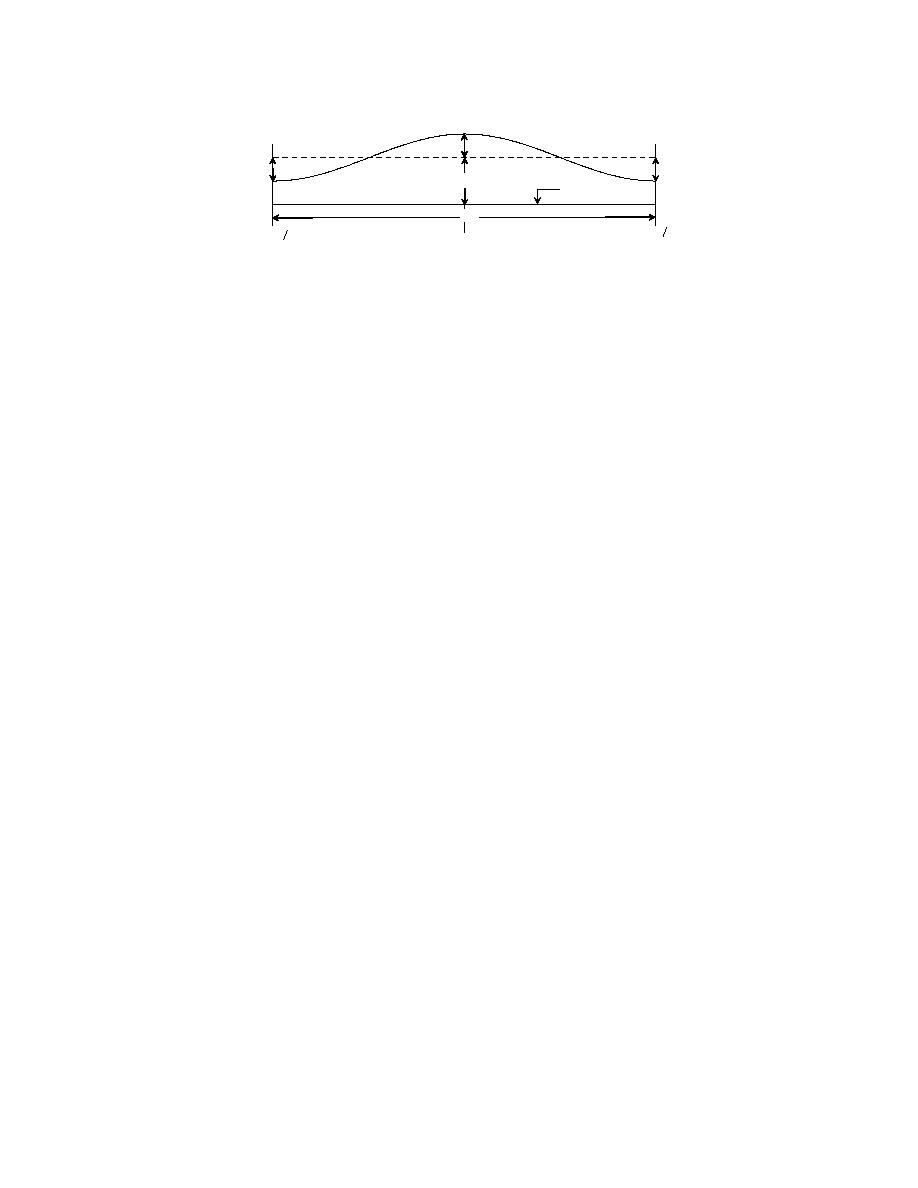
A1
A1
A1
A0
η =0
λ
x=λ 2
x = -λ 2
x=0
Fig. 5: Cross section of the initial condition for Exner's "dune problem" as defined by Eq. (25)
We solve this one-dimesional problem over a two-dimensional domain using four
different grids with uniform nodal spacing of h = 1, 0.5, 0.25, and 0.125. We compute the
maximum or L∞ norm by comparing our DG solutions to the exact solution. In Fig. 6, we plot h
versus the maximum error norm on a log-log scale where it can be observed that the theoretical
convergence rate of p+1 is obtained. Both the numerical and exact solutions of the evolution of
the mound at a cross section taken along the x-axis are shown at two different times in Fig. 7.
The solutions indicate that the mound develops into a dune-like shape with a gentle upstream
slope followed by a steeper downstream slope that becomes progressively steeper in time. It
should be noted how well the DG solution captures the steep downstream slope of the dune
without the introduction of any spurious spatial oscillations or any significant numerical damping.
21




 Previous Page
Previous Page
