constituted permutations of the following target parameter values: Hmo = 3.7
and 5.5 cm, Tp = 0.7 and 1.4 s, wave direction perpendicular to the jetties, and
Uc = 0, 12, and 24 cm/s. Wave height and current were measured at several
gauges placed around the inlet with the main objective of studying wave
breaking and to determine the wave height decay.
Here, four runs were simulated to investigate the model performance,
especially regarding the capability of (a) the wave action equation (Equation
1) to reproduce the wave transformation in the presence of a current using
linear wave theory, (b) the criterion for incipient breaking (Equation 12) to
describe waves propagating on a current and in limited water depth, and (c)
the generalization of Dally's model (Equations 13-16) to predict the energy
dissipation due to wave breaking on a current.
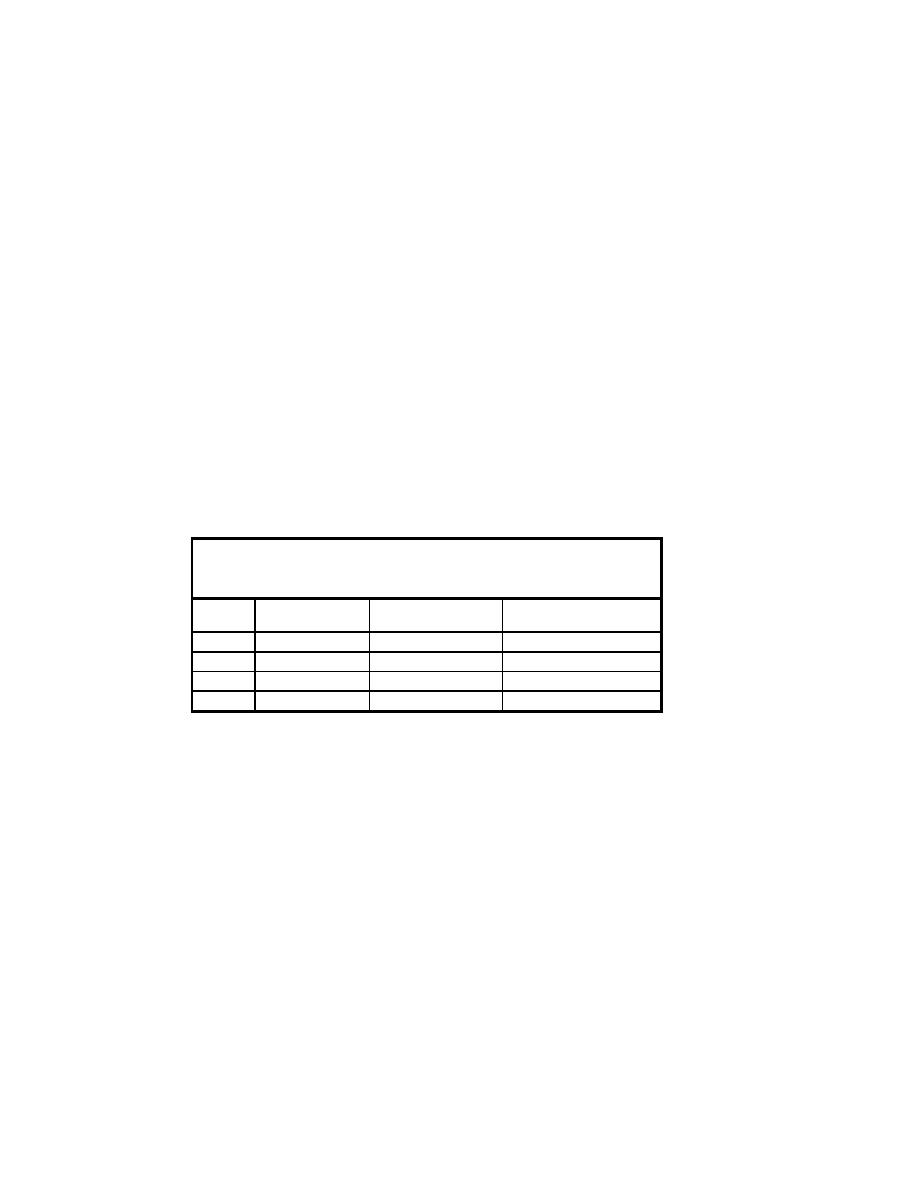
Table 1 summarizes the runs selected for simulation representing both
long- and short-period wave cases, as well as, weaker and stronger currents.
The values given in the table are the target values, whereas for the model
simulations the actual measured wave heights and periods in the horizontal
portion of the basin (just off the wave maker) were employed (see
Appendix A in Smith et al. 1998). The conditions of the CHL-I experiments
were such that blocking should not occur according to the criterion based on
linear theory (Equation 19) with the peak spectral wave period characterizing
the waves. The measured wave heights in the experiments indicate that this
was indeed the case.
Table 1
Target Wave Conditions for Selected Runs from Smith et al.
(1998) Experiments Used in NMLong-CW Simulations
Significant
Peak Spectral Wave
Run
Wave Height (m)
Period (s)
Mean Current (m/s)
5
0.055
1.4
0.14
7
0.055
1.4
0.24
9
0.055
0.7
0.14
11
0.055
0.7
0.24
Standard values were employed for the coefficients in the wave
Γ = 0.4. Waves were represented by a Monte-Carlo simulation by assuming
a Rayleigh pdf in the offshore (i.e., in the horizontal portion of the basin
where wave breaking and the current were negligible). NMLong-CW
normally provides the root-mean-square (rms) wave height as output since
this quantity may be calculated in a straightforward manner without having to
save all intermediate calculation results from individual waves in the
ensemble representing the offshore pdf. However, Smith et al. (1998) only
reported the energy-based significant wave height Hmo, so the entire
simulated series of waves at each location were run in the present cases to
compute the significant wave height by taking the mean of the one-third
largest waves (assumed to be equal to the spectrally determined zero-moment
wave height Hmo reported for the experiments).
The measured current at six locations defined the input cross-shore
current distribution. Linear interpolation was employed between the
measurement points to obtain values at the different model grid points.
However, because no measurements of the current were made at some
distance seaward of the inlet mouth (except close to the wave maker where
26
Chapter 4 Verification of Wave Model




 Previous Page
Previous Page
