S.A. Hughes / Coastal Engineering 51 (2004) 10851104
1093
the slope. In this section, a simple derivation is
equation based on the dimensionless maximum wave
performed based on this assumption.
momentum flux parameter, i.e.,
!1=2
1=2
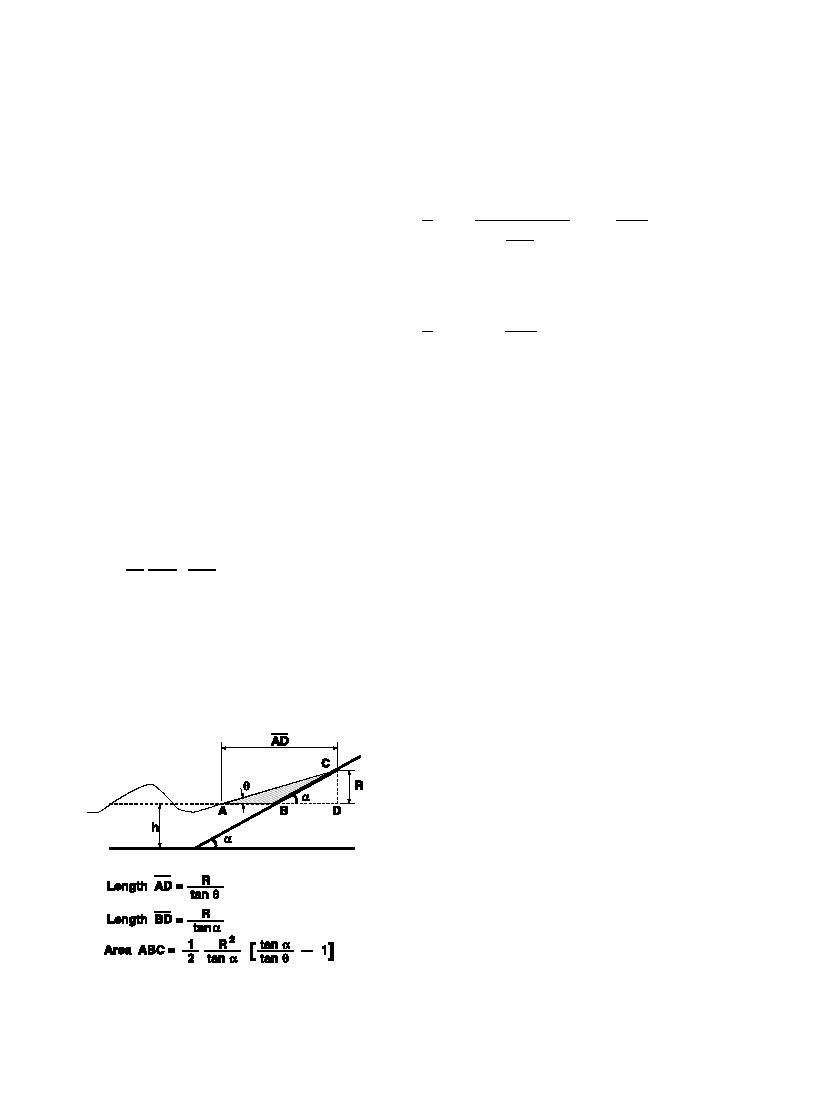
geometry at the point of maximum wave run-up. The
2KPtana
R
MF
!
36
force of the wave has bpushedQ the water up the
qgh2
tana
h
1
KM
impermeable slope. At the instant of maximum run-
tanh
up, the fluid within the hatched area on Fig. 2 has
almost no motion. (Li and Raichlen, 2002 noted this
or more simply
was nearly the case for solitary wave run-up.)
!1=2
Following the lead of Archetti and Brocchini (2002),
R
MF
CF a
37
a simple physical argument is that the weight of the
qgh2
h
fluid contained in the hatched wedge area ABC
where C is an unknown constant and F(a) is a
(W(ABC)) is proportional to the maximum depth-
function of slope angle to be determined empirically.
integrated wave momentum flux of the wave before
For convenience, the bmaxQ subscript has been
it reached the toe of the structure slope, i.e.,
dropped from the wave momentum flux parameter.
KPMFmax KMWABC
34
In the new run-up equation relative run-up (R/h) is
directly proportional to the square root of the wave
where KM is an unknown constant of proportionality
momentum flux parameter. Representing the run-up
and KP is a reduction factor to account for slope
sea surface slope as a straight line is an approximation,
porosity (KP=1 for impermeable slopes).
but, for waves on gentle slopes were wave breaking has
The weight of water per unit width contained in
occurred, this might be a reasonable assumption as
triangle ABC shown on Fig. 2 is given by
!
shown by Li (2000). On steeper slopes where waves
qg R2 tana
behave more like surging breakers, the sea surface
1
35
WABC
2 tana tanh
elevation will have more of a concave shape, also
illustrated by Li. Another simplification in this deriva-
where R is maximum vertical run-up elevation from
tion is the absence of slope friction, and this was shown
SWL, a is structure slope angle, and h is an unknown
by Archetti and Brocchini (2002) to be important for
angle between still water level and run-up water
swash zone run-up processes on mild slopes where the
surface (which is assumed to be a straight line).
wave travels over a much longer distance.
Substituting Eq. (35) into Eq. (34), rearranging and
dividing both sides by h2 yields a new run-up
3.2. Regular wave run-up
The proposed run-up relationship given by Eq. (37)
was empirically fit to existing regular wave run-up
laboratory test results published many years ago by
impermeable-slope tests, waves propagated over a flat
bottom before reaching a linear slope that was varied
between 158 and vertical. Wave heights were some-
what mild with maximum relative wave height of
H/hc0.35. A total of 52 run-up values for slopes
ranging over cota=1.00, 1.43, 1.73, 2.14, 2.75 and
3.73 are used in this reanalysis.
Most of the waves in the experiments reported by
before reaching the impermeable structure slope. Run-
Fig. 2. Maximum wave run-up on a smooth impermeable plane
up values were reported for slopes with cota=2.0, 3.0,
slope.





 Previous Page
Previous Page
