1100
S.A. Hughes / Coastal Engineering 51 (2004) 10851104
triangular wedge derivation presented earlier is not
and predicted R/h was 0.12 for all data, and the RMS
appropriate for steeper slopes and a more accurate
error dropped to 0.034 when the three out-lying points
description of the wedge volume is needed. Never-
were discarded. Also note that structure slope has a
theless, Eq. (43) yielded reasonable estimates for
relatively minor influence for nonbreaking solitary
slopes between 1/30 and 1/10.
waves.
A theoretical run-up equation for nonbreaking
3.4.2. Nonbreaking Solitary Wave Run-up
solitary waves was presented by Li and Raichlen
Nonbreaking wave run-up data from Synolakis
(2001) as
(1986, 1987) for a plane impermeable slope with
5=4
cota=2.08, and data from Hall and Watts (1953) for
R
H
1=2
2:831cota
slopes with cot a=1.0, 2.14 and 3.73 were used to
h
h
Li
examine the utility of the wave momentum flux
9=4
H
parameter for estimating nonbreaking solitary wave
3=2
0:293cota
45
run-up. In this case, relative wave run-up R/h was
h
shown to be directly proportional to the maximum
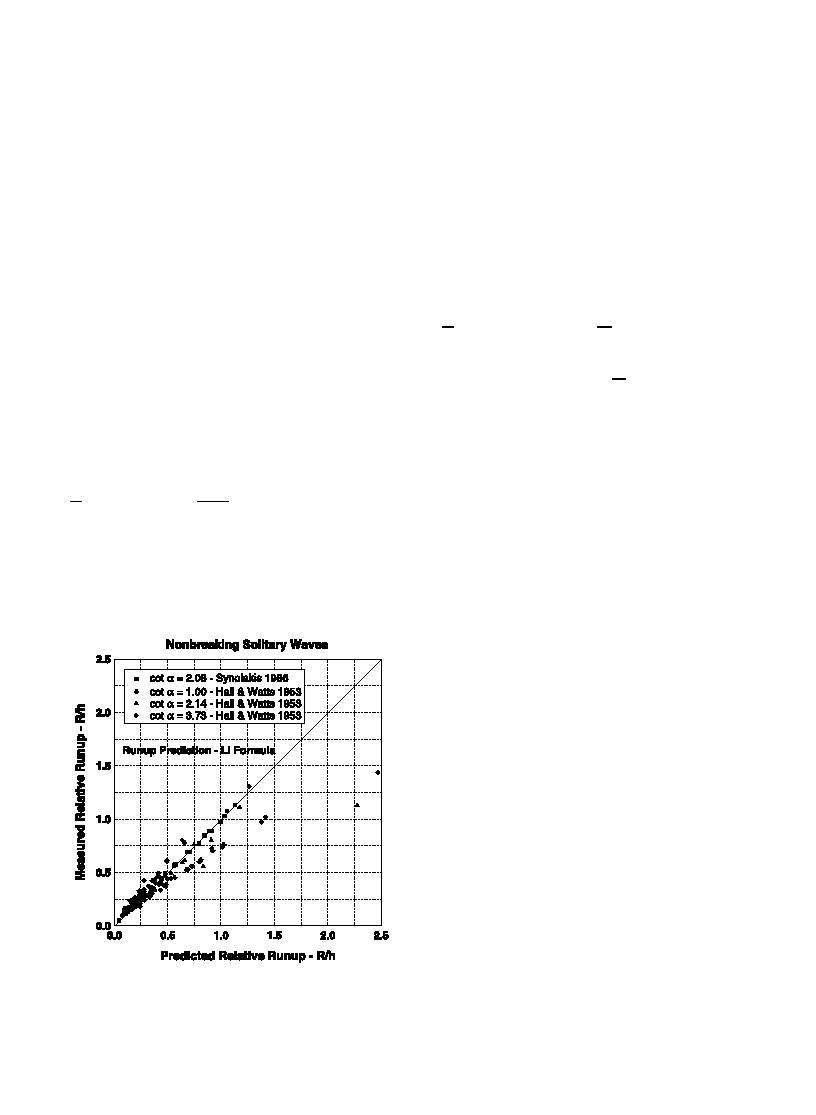
Predictions using Eq. (45) are compared to the
depth-integrated wave momentum flux parameter with
a very good fit to the 122 data points provided by the
nonbreaking run-up data in Fig. 13. Good corre-
spondence is seen except for the milder slope
with cota=3.73. It is interesting to note that
R
MF
substitution of Eq. (31) for MF/(qgh2) in Eq. (44)
1:82cota1=5
44
qgh2
h
results in an expression containing terms with H/h
raised to powers that are approximately the same as in
Goodness-of-fit is shown in Fig. 12 for the nonbreaking
Eq. (45).
wave run-up data. With the exception of a few outlying
points, the empirical Eq. (44) does remarkably well.
Overall root-mean-squared error between measured
4. Summary and conclusions
The goal of this study was to develop new
formulas for wave run-up on smooth, impermeable
plane slopes based on a new parameter representing
the maximum depth-integrated wave momentum flux
occurring in a wave. These formulas should be as
good as existing formulas for estimating run-up due to
waves that break on the slope and better at estimating
nonbreaking wave run-up.
A crude run-up formula was derived based on the
simple argument that the weight of water contained in
the run-up wedge above still water level at maximum
run-up is proportional to the maximum depth-inte-
grated wave momentum flux in the wave at or near the
toe of the slope. The derived general formula included
an unknown function of slope that needed to be
determined empirically.
Existing published wave run-up data for regular,
irregular and solitary waves were used to establish
the empirical slope functions for the new wave run-
up formulas. Reasonable predictive capability for
Fig. 13. Measured versus predicted nonbreaking solitary wave run-
regular waves was demonstrated for all but the
up--Li formula.




 Previous Page
Previous Page
