equation gives the following equation to solve with the water depth at breaking as the
unknown,
5/ 2
2
hb H o cos θo
hb
cos arcsin 2π sin θo
=
(9)
2
Lo Lo γb 2 2π
Lo
height to water depth at incipient breaking (taken to be 0.78). This equation shows that
hb/Lo (or, equivalently hb/Ho) is a function only of Ho/Lo and θo. A look-up table is
employed to quickly obtain hb from known input wave properties. Once hb is obtained, the
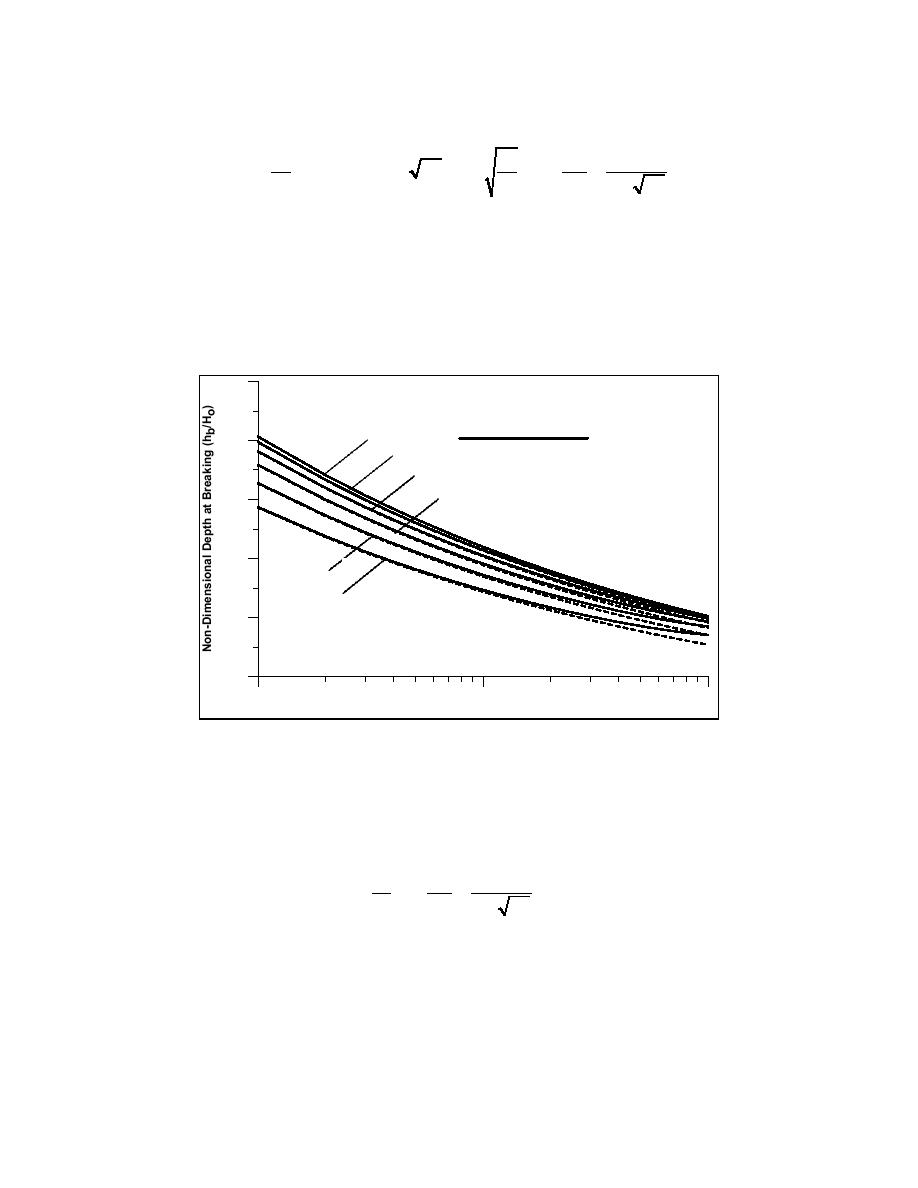
other quantities at the break point may be calculated directly. Fig. 2 illustrates the variation
of hb/Ho with Ho/Lo and θo (solid lines).
3.0
10 deg
Deepwater Wave Angle
2.5
20 deg
30 deg
40 deg
2.0
1.5
50 deg
60 deg
1.0
0.5
0.00
0.01
0.10
Deepwater Wave Steepness (Ho/Lo)
Fig. 2. Normalized depth at breaking as a function of wave steepness and angle in deep water
(exact and approximate solutions).
If the wave angle at breaking is small, cos θb ≅ 1.0, and hb can be calculated explicitly
from:
2/5
hb H o cos θo
2
=
(10)
Lo γb 2 2π
Lo
2
Fig. 2 also includes solutions for this approximate expression (broken lines), indicating that
θo (calculations showed that the error is maximum 10% for all angles and steepnesses).
The wave angle at the break point is calculated from Snell's law:
Larson, Kraus, and Hanson
5




 Previous Page
Previous Page
