The mixing coefficient given by Equation 45 is in principle the same as
that derived by Battjes (1975), if gβDmR is identified as the mean rate of wave
energy dissipation per unit area. The empirical coefficients in front of the
bracket on the right side of Equation 45 yield a value of about unity by
applying values from typical turbulent flows (Rodi 1980). In NMLong-CW,
to take into account the enhanced mixing from wave breaking, test
simulations were carried out with the following equation:
1/ 3
gβ m
ε = Λ1Hum + Λ2 D R
(46)
d
ρ
where Λ1 and Λ2 are nondimensional coefficients.
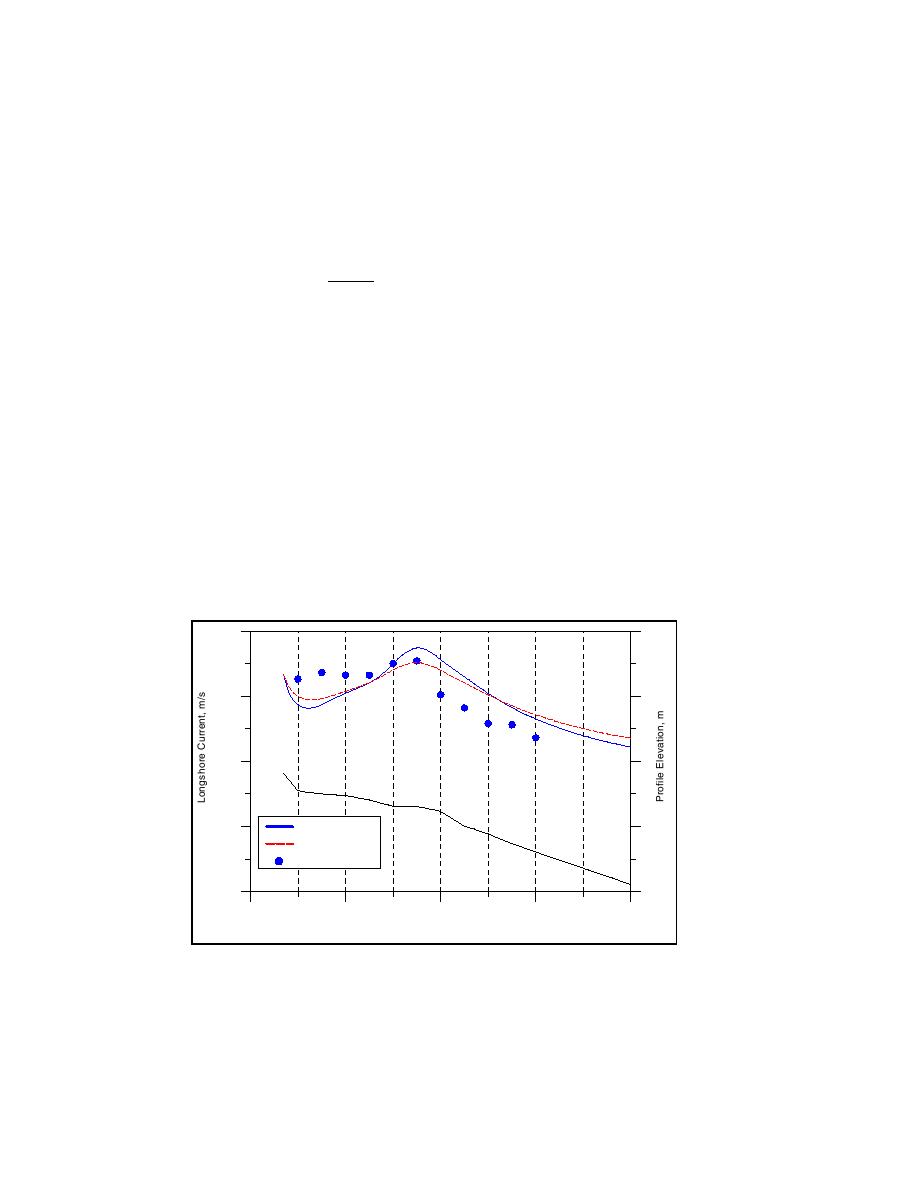
The two coefficients were given the same value in the test simulations,
namely Λ1 = Λ2 = 0.5. Figure 41 displays the result of introducing the
additional mixing, where a general decrease in the current speed occurred
compared to the standard mixing. A slight increase in velocity close to shore
is noted, as well as a tailing off in deeper water with a smaller gradient.
However, the result does not show marked improvement over the standard
agreement in the surf zone, and the current distribution could be made close
to flat here in agreement with the data. Simultaneously, the offshore tail in
the current distribution will decrease less steeply, implying worse agreement
in this region. Thus, in summary, it is difficult to reproduce the measured
current distribution through enhanced mixing, at least if the preceding
expressions are employed.
1.0
2
0.5
1
0.0
0
Standard mixing
-0.5
-1
Beach Profile
Enhanced mixing
Measured
-1.0
-2
0
20
40
60
80
Distance Across Shore, m
Figure 41. Calculated (two different mixing formulations) and measured
longshore current for Kraus and Sasaki (1979) field experiment
(beach profile also shown for calculation domain)
62
Chapter 6 Verification of Longshore Current Model




 Previous Page
Previous Page
