62
F.S. Buonaiuto, N.C. Kraus / Coastal Engineering 48 (2003) 5165
annual deepwater significant wave height (m). The
Because the limiting depth over an ebb shoal is
factor of 3.6 in front of the wave height in Eq. (3) for
controlled by both wave height and tidal prism, a
ebb shoals is much larger than that for the depth over
combination of those two quantities might have
crest for depth-limited waves breaking on longshore
greater predictive power. For this purpose, the param-
eter (HSP)1/4 is introduced that has units of length (m).
bars (which is 0.66; see Larson and Kraus, 1989)
because of the erosion by the ebb jet. Although Eq. (3)
Regression with an assumed linear dependence yields:
predicts depth over the crest of the main ebb shoal
hC 0:066 0:046HSP1=4
MLLW
5
six data points fall outside of the 95% confidence
intervals. Also, the relatively large constant or inter-
which has an intercept of 0.066 m that is consid-
cept, 0.27 m, suggests that a pertinent governing
erably less than the uncertainty in individual depth
process is omitted, such as the tidal prism.
soundings, and Eq. (5) is convenient in having homo-
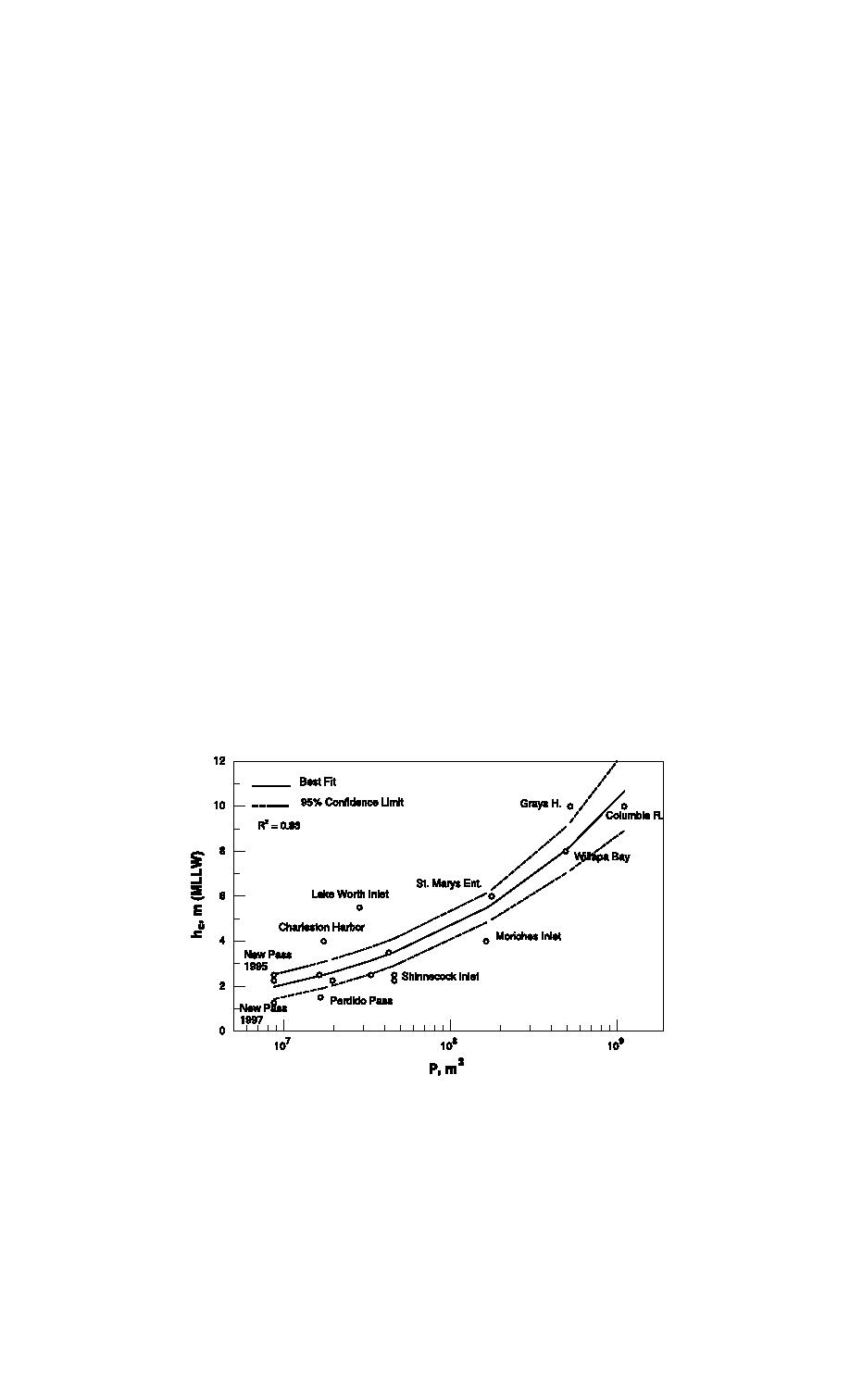
The seaward extent of the ebb shoal is known to
genous units. Six data points remain outside of the
depend on the tidal prism P (Floyd, 1968), so the
confidence limits (Fig. 10), and the bands are tighter
depth over ebb-shoal crest was regressed with a
to the regression line (R2 = 0.87) than in Figs. 8 and 9.
power-law form similar to those listed in Table 1,
The three regression equations account for the
namely hC = CPn, giving:
variance in the data set reasonably well. The depth
to the ebb-shoal crest was marginally better predicted
hC 0:0063P0:35
MLLW
4
by the combination of the incident wave height and
tidal prism (Fig. 10), based upon R2 values and cluster
with R2 = 0.83, but with eight data points lying outside
within the 95% confidence limits. Homogeneous units
the 95% confidence limits (Fig. 9). Eq. (4) is not
and scaled magnitude (reasonable magnitude of val-
ues) of the parameter (HSP)1/4 make it convenient for
convenient because of the awkward dimensional
empirical coefficient.
calculations.
Fig. 9. Power law regression between the depth over crest of an ebb shoal and tidal prism.




 Previous Page
Previous Page
