In the original morphologic model (Kraus 2003), the transport rates were
^
^
^
parameterized as QS = QS (1 - x / xe ) and QB = QB (1 - z / ze ) , in which QS and
^
QB are constant maximum rates assumed to occur at the start of the breach, and
breach-forcing conditions. Closed-form solution of the two equations was
^
^
^
found possible if QB and QS equaled a constant rate Q , leading to solutions of
the form x = xe [1 - f ( x) exp(-t / τ)] and z = ze [1 - g ( z) exp(-t / τ)] . These
solutions describe an exponential growth toward equilibrium at a rate governed
^
by the morphologic time scale τ = xe ze L / Q . Eqs. (1) and (2) possess
characteristics encountered in chaos theory. Therefore, the solution at early
stages strongly depends on the initial condition, contained in the functions f and
g, but reaches the same value in exponential growth toward equilibrium.
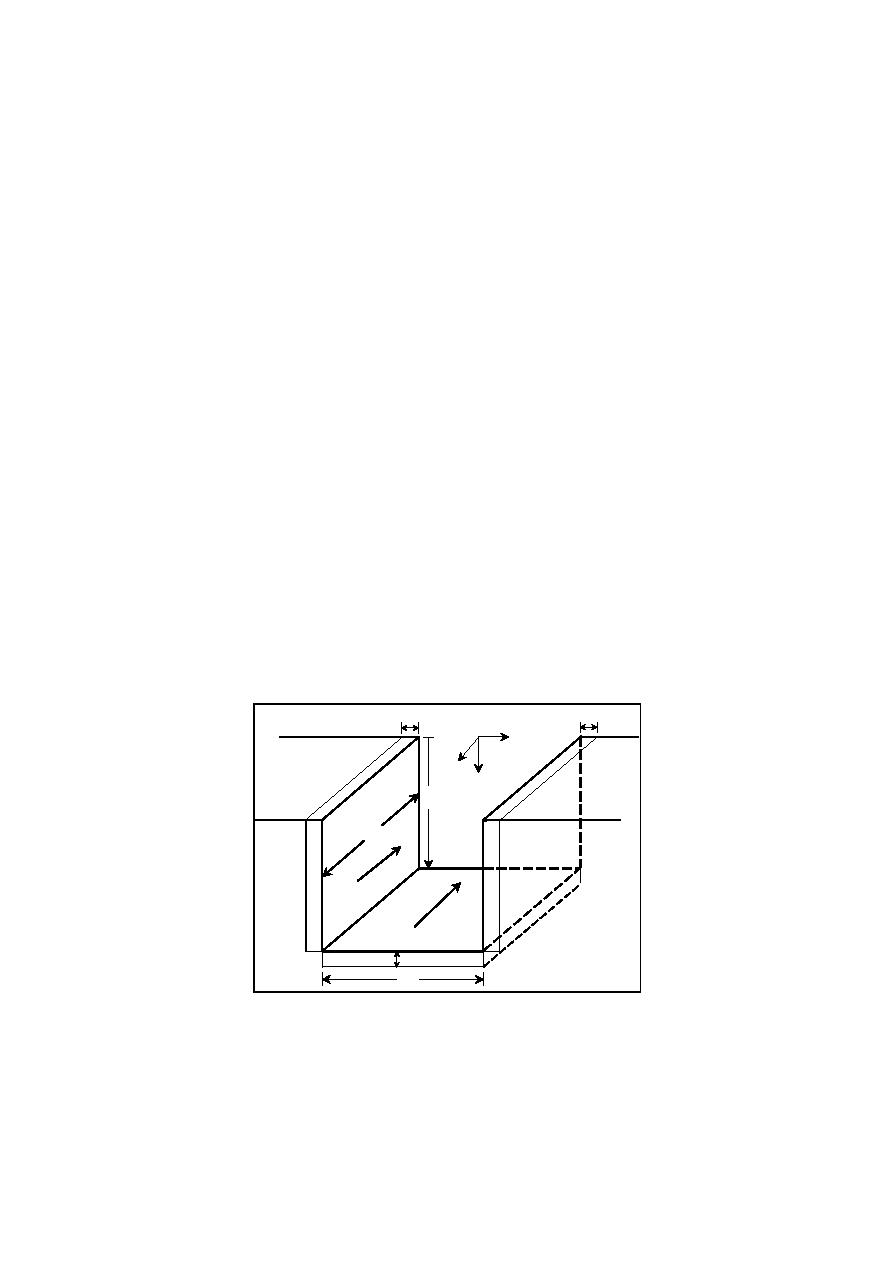
The original morphologic model represents the macro-scale process of
breach growth. The solution indicates time-dependent breach dimensions are
controlled by seven variables: initial width and depth of the breach, equilibrium
width and depth of the breach, width of the barrier island, and maximum or
initial net sediment transport rates at the bottom and sides of the breach.
The original model was limited in not accounting for the current that
transports sediment through the breach. The breaching model is extended here
by incorporating a 1-D inlet hydrodynamic model to calculate sediment
transport, as well as including longshore sediment transport and wave set up.
∆x
∆x
x
y
z
z
L
QS
QB
∆z
x
Figure 1. Definition sketch for rectangular barrier island.
3




 Previous Page
Previous Page
