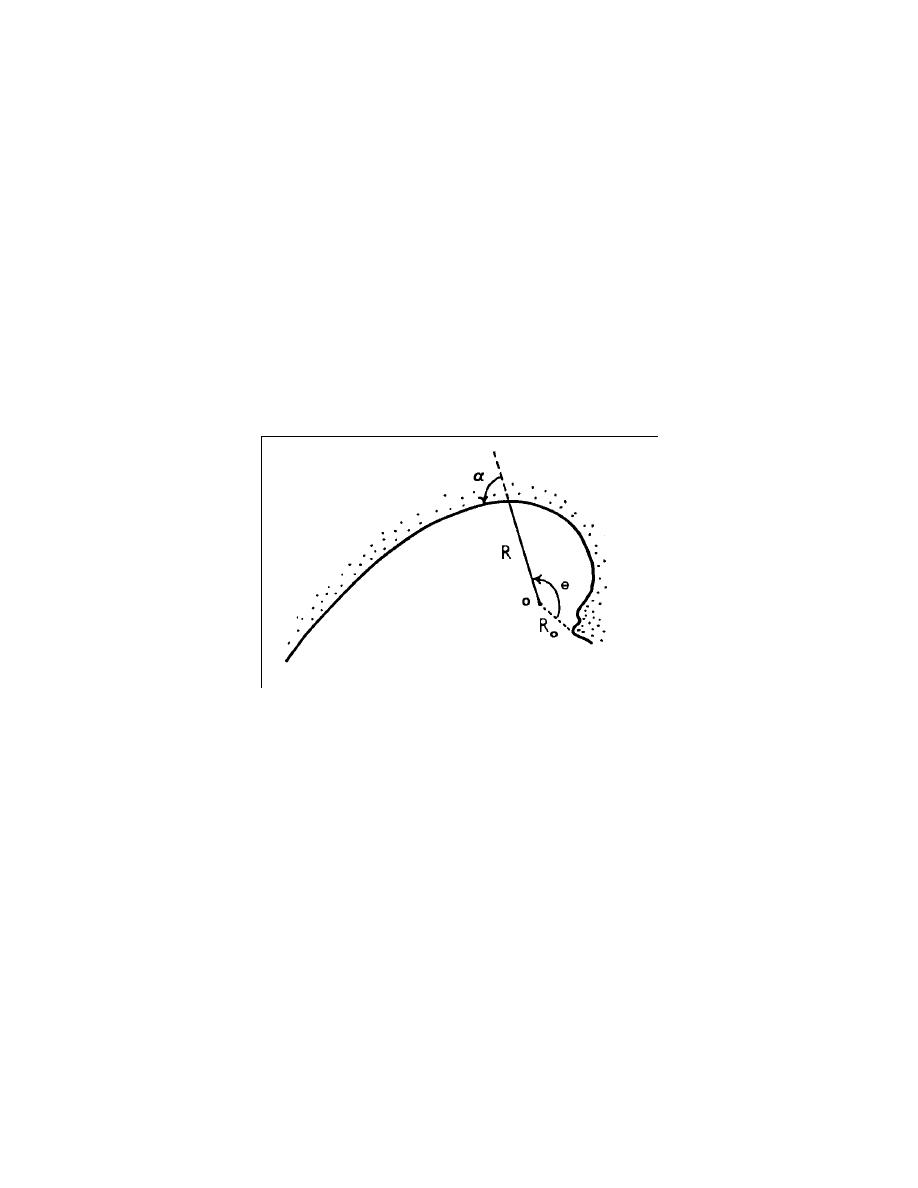
where R = length of the radius vector for a point P measured from the pole O; θ = angle
from an arbitrary origin of angle measurement to the radius vector of the point P; R0 =
length of radius to arbitrary origin of angle measurement; and α = characteristic constant
angle between the tangent to the curve and radius at any point along the spiral.
A property of the log-spiral curve is that the angle a between the tangent to the curve
and the vector radius at any point along the curve is constant. This leads to the
interesting result that the shape of the log spiral is controlled only by α, with the
parameter Ro determining the scale of the shape. In fact, the functioning of Ro is
equivalent to setting a different origin of measurement of the angle θ. In other words,
graphically the log-spiral may be scaled up or down by turning the shape around its pole.
Fig. 2 shows how different values of α alter the shape.
Fig. 1. Definition sketch of the logarithmic spiral shape.
Values of α for headland-bay beaches reported in the literature range from about 45
to 75. In general, as α becomes smaller, the log spiral becomes wider or more open.
There are two singular values or limits for α: if α = 90, the log spiral becomes a circle,
and if α = 0, the log spiral becomes a straight line.
Sensitivity of the log-spiral shape to small changes in α is shown in Fig. 3. Variations
( 1%) in α-values produce large variations in position of the spiral, because the angle
enters the argument of an exponential function. Additionally, the smaller the
characteristic angle α, the larger the difference for the same percentage of angle
variability. The practical consequence is that, because we are interested in fitting this
log-spiral shape to headland-bay beaches especially in design of shore-protection
projects, α has to be accurately defined.
Moreno & Kraus
4




 Previous Page
Previous Page
