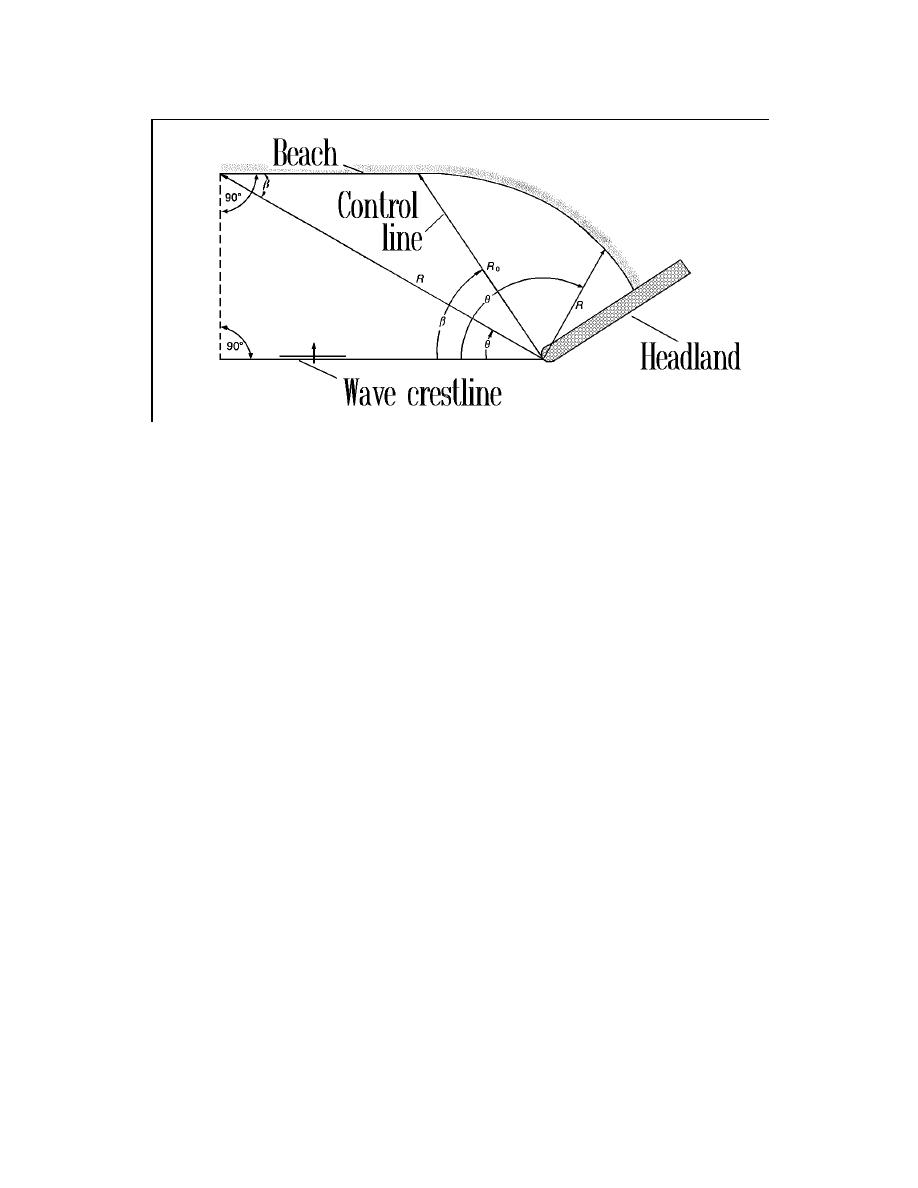
Fig. 4. Definition sketch of the parabolic shape.
Fig. 5 depicts change in parabolic shape for different values of for fixed R0 and a
given focus position. Because the parabolic shape is defined only for ? ≥ , the
alongshore extent of the shape decreases as β increases. In addition, as β increases, the
slope of the shape at the point where θ = β departs farther from horizontal. Similarly,
Fig. 6 shows the change in parabolic shape for different values of Ro for constant , for
a given focus position. The scaling effect of the radius Ro is evident. In summary, the
angle controls the shape of the parabola, and Ro controls its size.
Because the control line intersects the beach at the point where the curved section
meets the straight section of the beach, the sensitivity of the parabolic shape to errors in
the estimation of the control point was examined. This was done by jointly changing Ro
and while keeping the distance from the headland to the straight shoreline constant.
Fig. 7 shows the resultant parabolic shapes for slightly different locations of the
control point. It is apparent that the parabolic shape is insensitive to . This observation
means that the control point is not well defined, i.e., uncertainty in selection of the
control point and hence the radius Ro and has little influence on the final result.
To analyze the validity of the assumption that a parabolic shape can describe
headland-bay beaches, the location of the focus of the parabola and the characteristic
angle must be specified, together with the scaling parameter Ro. Because the parabolic
shape is defined in a particular coordinate system, in design applications an extra
unknown enters the orientation of the entire parabolic shape in plan view. Therefore,
five unknowns must be solved for in practical applications. For this purpose, a computer
program was prepared that solves for the five unknowns by minimizing the composite
radial (for the curved section of the beach) and Cartesian (for the straight-line section of
the beach) rms error of fit for a given bay-shaped beach.
Moreno & Kraus
7




 Previous Page
Previous Page
