found that growth of the platform preceded formation of the spit. Here, the term
"spit" will represent both the subaerial ridge and platform, unless otherwise stated.
a
(a) Cross -
Qout
Qin
section view
B
∇
∆x
D
DC
x
Qin
Qout
∆x
(b) Plan view
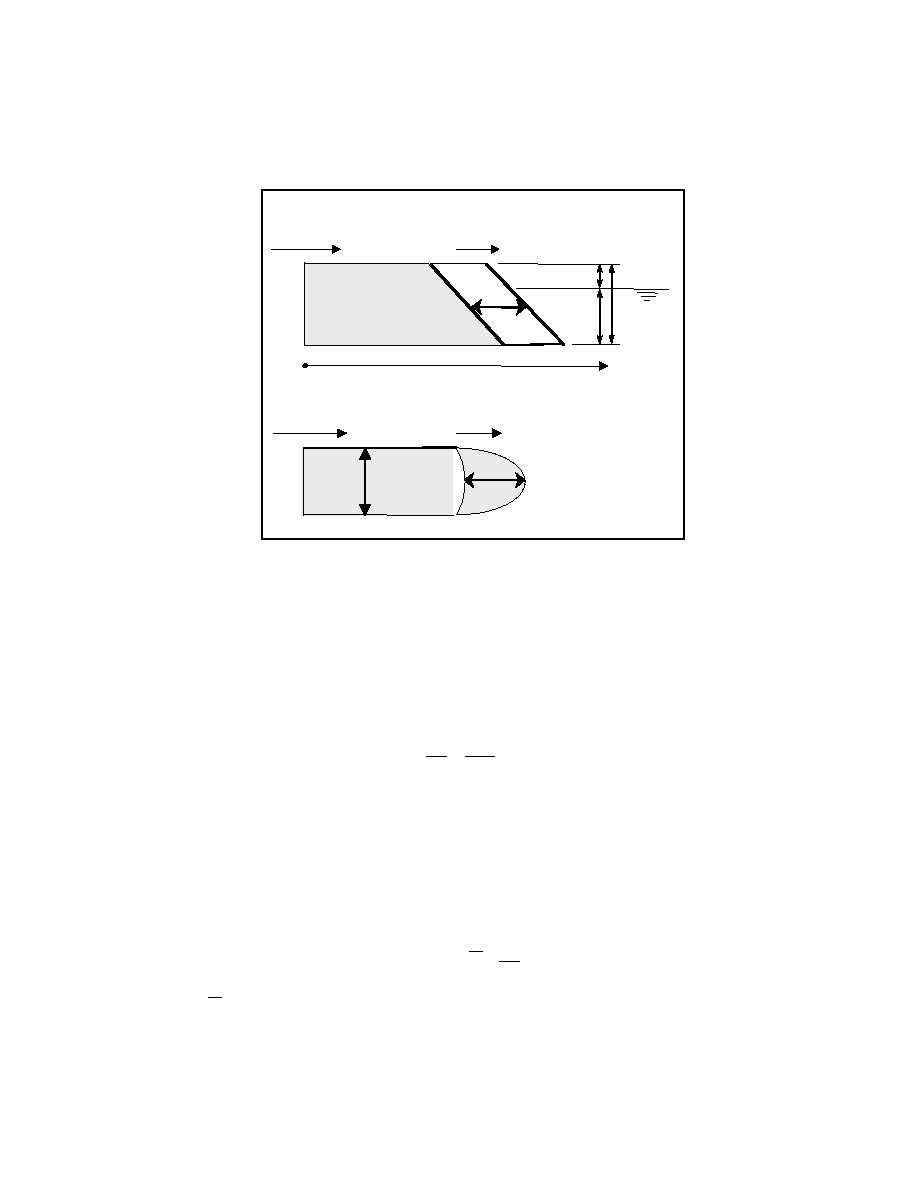
W
Fig. 1. Definition sketch for analytical model of spit elongation.
Viewing Fig. 1, in time interval ∆t, the volume change ∆V equals WD∆x, for
which the depth of active motion is D = B + DC (sum of the berm elevation and the
depth of closure); and ∆x is the increment of change in length of the spit in time ∆t.
By assumption, the volume change is equal to the volume entering minus that
leaving during the time interval, i.e., ∆t(Qin Qout). In the limit, the sand
conservation equation becomes
b
g
dx
1
=
Qin - Qout
(1)
dt WD
Solutions of the Eq. (1) are determined after specifying an initial condition,
boundary condition and functional forms for the transport rates and other parameters,
as appropriate. We now consider four examples of increasing complexity.
Example 1: Unrestricted Spit Growth
If a spit can elongate without restriction over the period under consideration, then
Qout = 0 (no sediment leaves or enters the spit from the distal end). Consider
Q′
Qin = Q +
cos(σt )
(2)
2
where Q = time-mean longshore sediment transport rate; Q′ = amplitude of a
/2
sinusoidal fluctuating rate; and σ = angular frequency of the motion, for example,
Kraus
4




 Previous Page
Previous Page
