Example 2: Spit Growth Restricted by Presence of Inlet Channel
As an inlet spit elongates, eventually its motion will be modified by the presence
of the inlet channel or of an obstacle. Encroachment of the spit to a channel will
tend to push the channel in the direction of spit migration, forcing the channel to
migrate as in the case of Democrat Point and Fire Island Inlet, as described in the
Introduction. On the other hand, the tidal current will tend to transport material off
the tip of the spit, slowing its growth as compared to that given in Eq. 3 for
unrestricted growth. At an inlet without stabilization structures, the competing
processes of channel infilling by longshore transport and of channel scour by tidal
and river discharge maintain a dynamic balance and equilibrium channel cross-
sectional area. This balance has been examined quantitatively by Kraus (1998).
A phenomenological means of representing the scouring action of the channel in
retarding spit growth is through an appropriate boundary condition for the transport
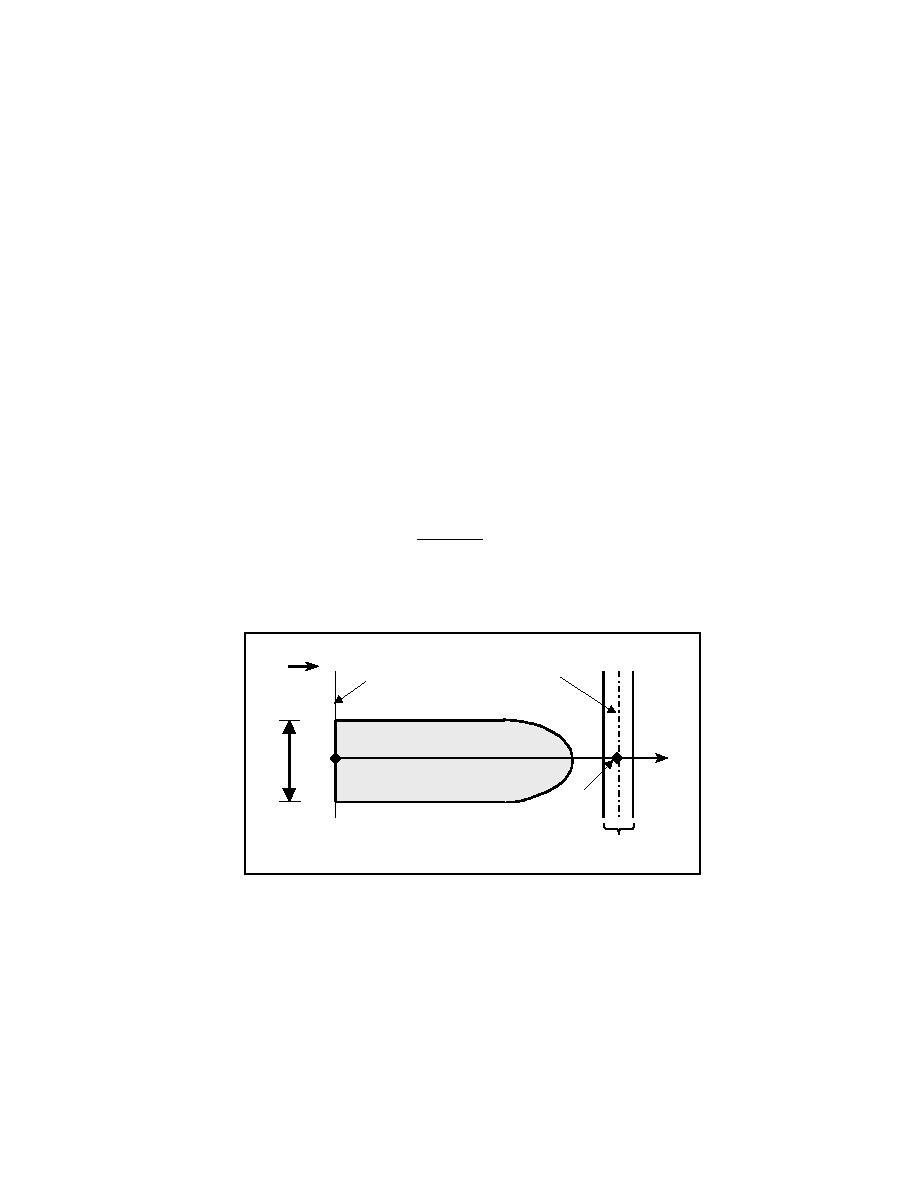
rate Qout. As one simple model of the boundary conditions, at a point xo located far
up-drift of the channel, the transport is unrestricted, so Qout = 0. At the location of
the channel (or another impediment to longshore transport), xC, the spit will not
elongate further if Qout = Qin. One simple representation of Qout between xo and xC is
to take a linear increase with distance moved toward the channel, as
bx - x g Q
Qout =
o
(4)
bx - x g
in
C
o
which satisfies the boundary conditions as stated. The situation is shown in Fig. 3.
Qout = Qin
Qin
Qout = 0
Spit
W
xo
x
xC
Inlet
Channel
Fig. 3. Definition sketch for spit approaching an inlet channel.
The solution of the governing equation (Eq. 1) for this situation of restricted
$
elongation with Qin = Q (constant transport rate) is
c
h
xS = xoe - t /τ + xC 1 - e - t /τ
(5)
where τ is a characteristic relaxation time for spit elongation given by
Kraus
6




 Previous Page
Previous Page
