S.A. Hughes / Coastal Engineering 51 (2004) 10671084
1075
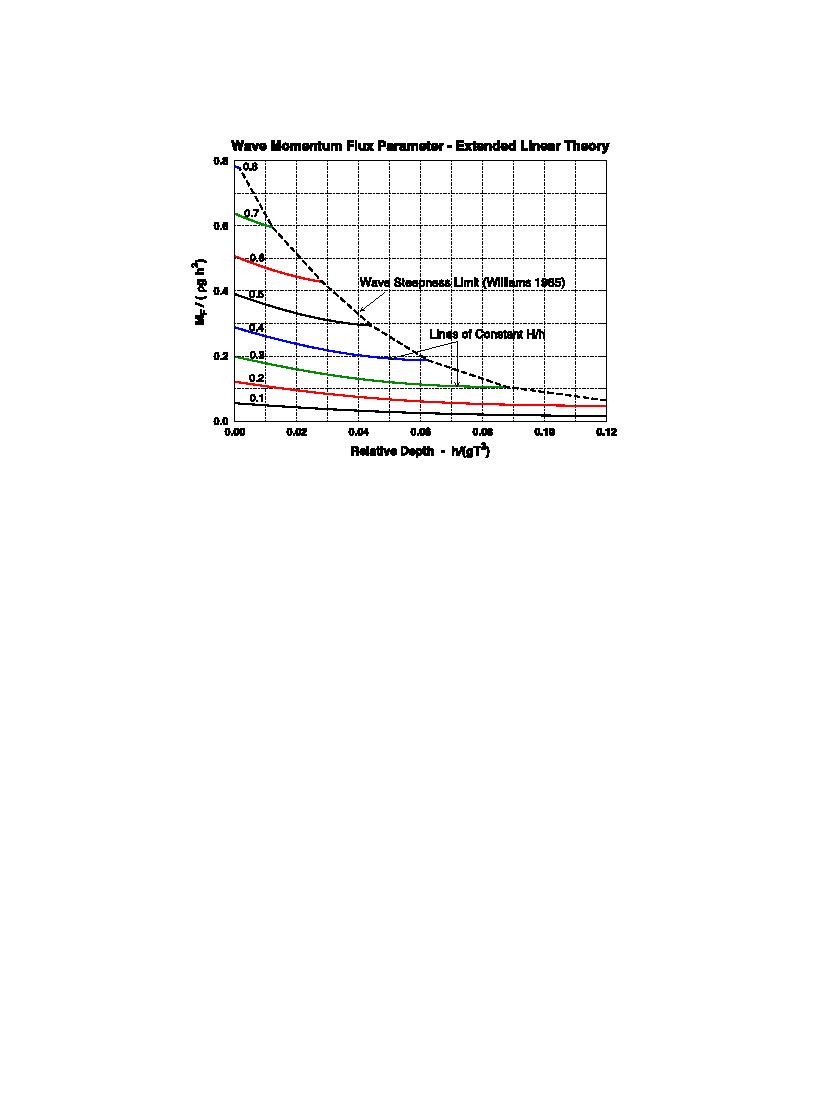
Fig. 3. Wave momentum flux parameter versus h/gT2 (extended linear wave theory).
the wave approaches its limiting relative wave height
given by Williams (1985), is shown by the dashed
(H/h).
line. Percentage contributions from the pressure and
Fourier approximation wave theory (Rienecker
horizontal velocity terms were similar to those noted
and Fenton, 1981; Fenton, 1988; Sobey, 1989)
for linear theory. As expected, estimates of maximum
provides good characterization of steady, finite-
depth-integrated wave momentum flux are greater
amplitude waves of permanent form over the entire
than corresponding estimates from linear theory with
range of water depths from deepwater to nearshore
the largest increase of almost 30% occurring for long
and for wave heights approaching the limiting steep-
waves near the steepness limit. Extended linear theory
ness. This hybrid analytical/computational method-
gives better estimates of (MF)max than linear theory,
ology represents the wave stream function by a
but it still does not account for wave asymmetry about
truncated Fourier series that exactly satisfies the field
the horizontal axis characterized by peaked crests and
equation (Laplace), the kinematic bottom boundary
long, shallow troughs typical of nonlinear waves.
condition, and the lateral periodicity boundary con-
ditions. Nonlinear optimization is used to complete
4.3. Nonlinear (Fourier) wave theory
the solution by determining values for the remaining
unknowns that best satisfy the nonlinear kinematic
Although linear and extended linear wave theories
and dynamic free surface boundary conditions
provide simple analytical estimates of maximum
(Sobey, 1989). Generally, more terms are needed in
depth-integrated wave momentum flux, experience
the truncated Fourier series to represent waves with
tells us that the momentum flux contained in the wave
pronounced asymmetry about the still water line, i.e.,
crest is crucial if we wish to relate this parameter to
steep waves and shallow water waves. Once the
the response of coastal structures in a realistic way.
coefficients of the Fourier series are established for a
The linear theory estimate of maximum wave
particular wave, the kinematics for the entire wave
momentum flux omits that portion of momentum flux
can be easily calculated.
above the still water line, and the extended linear
Because Fourier approximation wave theory pro-
theory neglects the effects of nonsinusoidal wave
vides complete kinematics for finite amplitude waves
forms typical of nonlinear, shallow water waves.
spanning the range covered by Stokes and Cnoidal
These omissions will become more problematic as




 Previous Page
Previous Page
