1078
S.A. Hughes / Coastal Engineering 51 (2004) 10671084
parts, but no uniform, clear consensus has been
found.
The wave momentum flux parameter represent-
ing an irregular wave train is probably best
specified by direct substitution of irregular wave
parameters into the empirical Eqs. (20), (21), and
(22) developed using Fourier approximation theory.
Application is simple, and estimates of maximum
wave momentum flux should be reasonably repre-
sentative of the irregular wave train. One drawback
to this method is inconsistency between investigators
regarding which irregular wave parameters to sub-
stitute. One application may use timedomain
statistics H1/3 and Tm, while another might use
frequencydomain parameters Hmo and Tp. Thus, it
is important to specify clearly which irregular wave
representative wave height and period are substi-
tuted. For now, the direct correspondence by
substitution of irregular wave parameters Hmo and
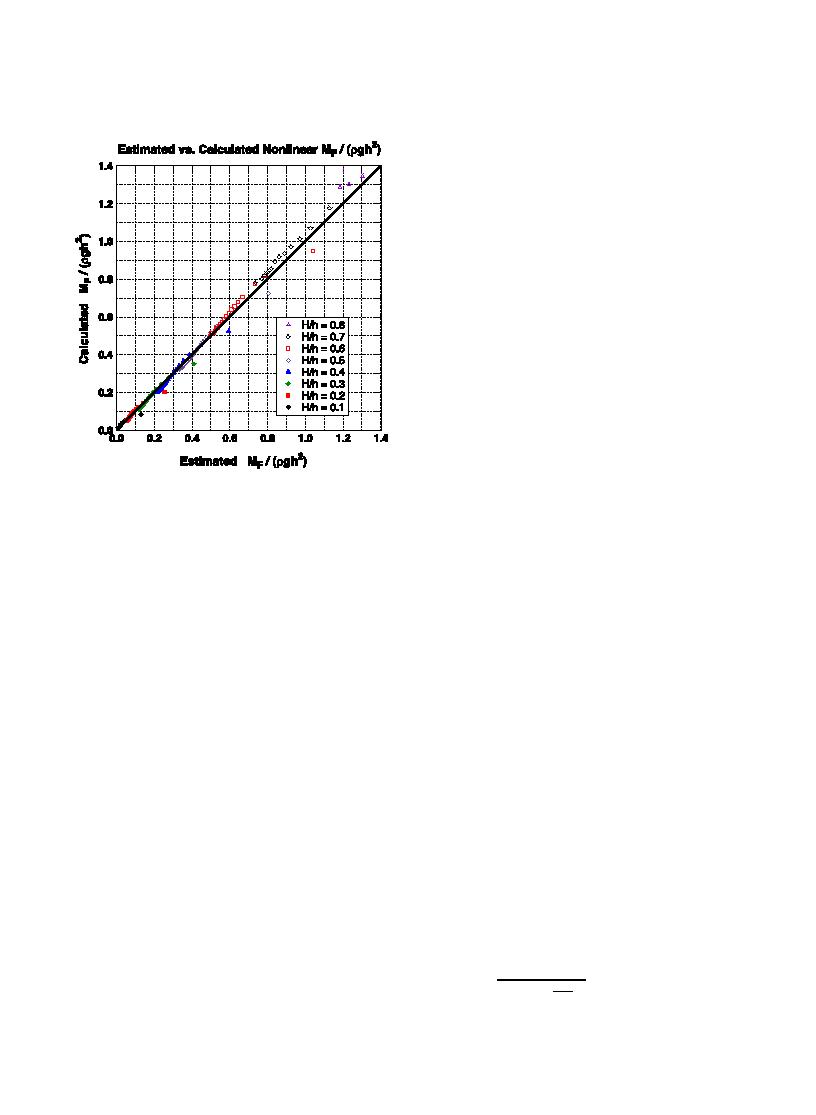
Fig. 6. Goodness-of-fit of nonlinear momentum flux empirical
Tp is recommended for estimating a value of the
equation (Fourier wave theory).
wave momentum flux parameter representative of
irregular waves.
or slightly above the limiting relative wave height
for waves on a horizontal seabed. This problem
was likely the result of forcing the numerical
5. Maximum wave momentum flux--transient
computation beyond appropriate limits. The maxi-
waves
mum underprediction and overprediction of the
empirical curve-fit were 0.105 and 0.089, respec-
Because the maximum, depth-integrated wave
tively. The overall root-mean-squared error of the
momentum flux can be determined for any wave
curve-fit was 0.023.
form in which the kinematics are known, it is
The empirical equation represented by Eq. (20),
possible to estimate the wave momentum flux
along with Eqs. (21) and (22), provides an easy
parameter for nonperiodic waves. This may prove
method for estimating the wave momentum flux
useful for comparing coastal process responses for
parameter for finite-amplitude, steady regular waves.
different wave types.
This empirical formulation is recommended over
those provided by linear and extended linear theory
5.1. Solitary wave theory
because it better represents the momentum flux in the
wave crest which is expected to be critical for most
The maximum depth-integrated wave momentum
applications to coastal structures.
flux of a solitary wave occurs at the crest where
both the horizontal velocity and dynamic pressure
4.4. Application to irregular waves
are greatest. To first-order of approximation, the
horizontal velocity at the crest as a function of
Most coastal structure design guidance developed
elevation zs above the bottom can be approximated
in the past 2025 years use wave parameters
as (e.g., Wiegel, 1964)
representative of unidirectional irregular wave trains
or, in rarer cases, directionally spread irregular
CN
waves. Attempts have been made to relate the
umaxzs
23
1 cosMhzs Š
irregular wave parameters to regular wave counter-




 Previous Page
Previous Page
