1076
S.A. Hughes / Coastal Engineering 51 (2004) 10671084
wave theories, it is possible to estimate reasonable
shows curves representing H/h=0.3 and 0.7. For the
values for maximum depth-integrated wave momen-
lower relative wave height of H/h=0.3, there is good
tum flux associated with these waves. Unfortunately,
correspondence between extended linear and Fourier
approximation for values of h/gT2 greater than about
such estimates of (MF)max must be calculated numeri-
cally which could significantly lessen the utility of the
0.03. As the relative depth decreases from 0.03, there
wave momentum flux parameter for design purposes.
is increasing divergence which illustrates the impor-
A simple empirical approximation for the wave
tance of nonlinear wave shape. Linear theory under
momentum flux parameter of finite amplitude waves
predicts extended linear theory by nearly a constant
was developed using a Fourier wave computer
amount.
program. This program was repeatedly run for
For relatively high waves (H/h=0.7), linear and
selected combinations of wave steepness (H/h) and
extended linear estimates clearly underpredict the
relative depth (h/gT2), and the resulting estimates of
correct value of the wave momentum flux parameter.
For example, at a value of h/gT2=0.01, the Fourier
wave kinematics were used to calculate maximum
depth-integrated wave momentum flux according to
approximation estimate of dimensionless (MF)max is
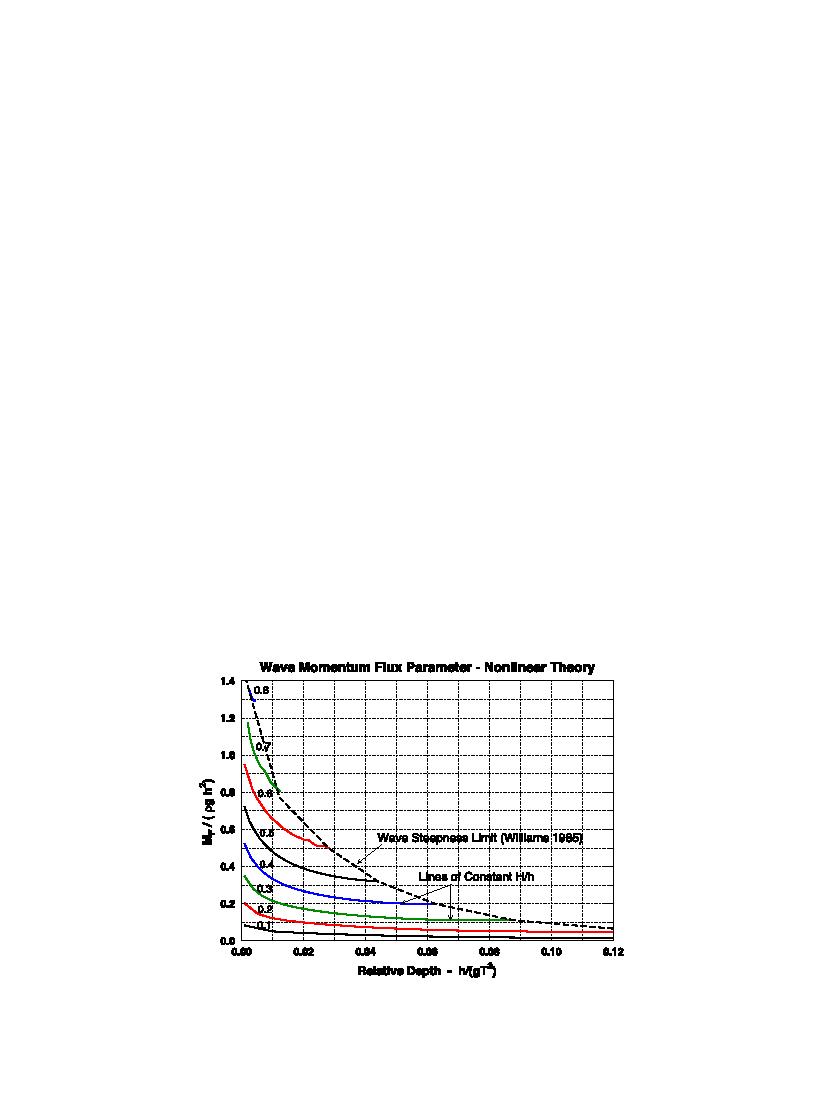
Eq. (7). Results are presented as the set of curves
2.0 times greater then the linear estimate and 1.4 times
shown on Fig. 4. Coding accuracy was checked by
greater than the extended linear estimate. This differ-
assuring that estimates of (MF)max for small ampli-
ence increases as relative depth decreases, emphasiz-
ing the importance of nonlinearities in nearshore
tude, deepwater waves were the same as estimates
waves.
given by the first-order analytical solution. In addi-
Application of the wave momentum flux parameter
tion, it was noted that estimates for very long waves
(small values of h /gT 2) approached the values
to coastal structure design and estimation of coastal
processes will typically involve empirical correlation
obtained from the analytical solitary wave solution
of the parameter with observed responses. It could be
given in the following section. The dashed line on the
argued that the empirical nature of this type of
plot represents the limiting wave steepness given by
application does not depend on absolute values but
rather on relative values of the incorporated wave
The difference between linear, extended linear, and
parameter; and in general, the linear and extended
finite-amplitude theory estimates of the wave momen-
linear curves show similar trends as the finite-
tum flux parameter is illustrated on Fig. 5 which
Fig. 4. Wave momentum flux parameter versus h/gT2 (Fourier wave theory).




 Previous Page
Previous Page
