S.A. Hughes / Coastal Engineering 51 (2004) 10851104
1091
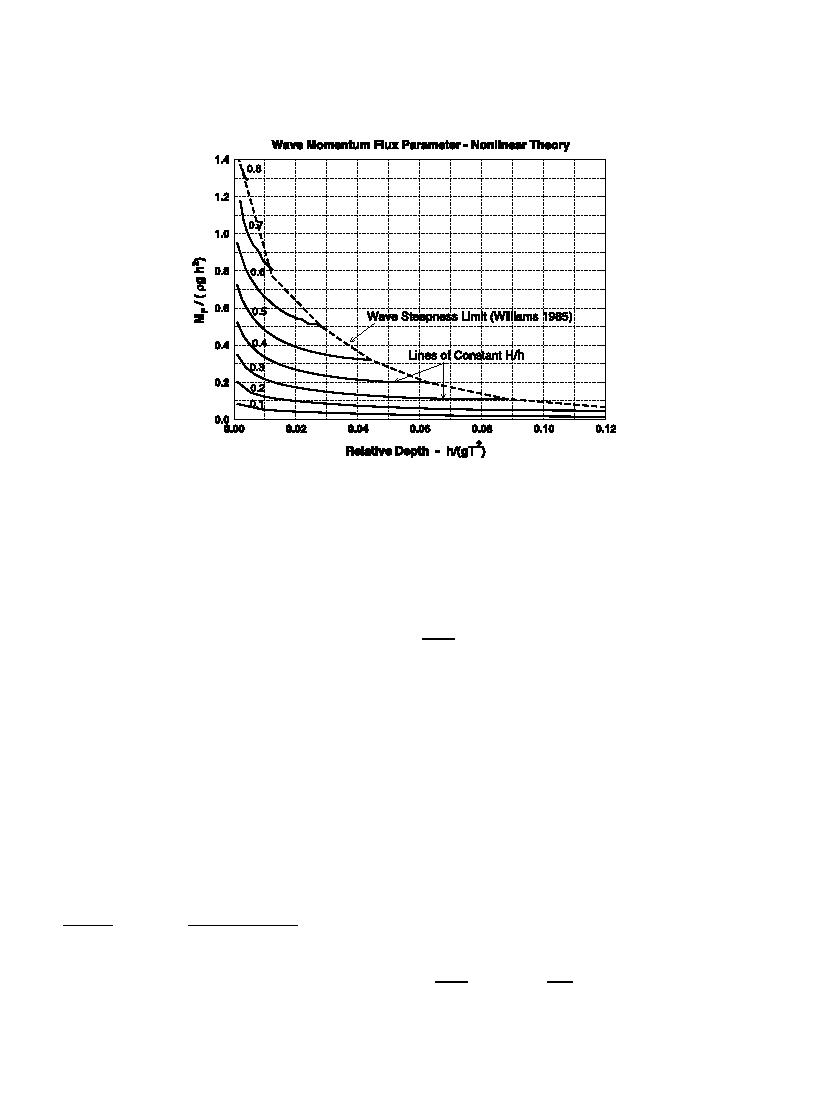
Fig. 1. Wave momentum flux parameter versus h/gT2 (Fourier wave theory).
under the crest when waves become nonlinear. For
the above expression has a maximum error of 0.0014
both linear and extended-linear theory, the relative
over the range of Williams' table. Williams' (1985)
contribution of the horizontal velocity term (qu2) to
tabulation of limit waves is more accurate than the
the total wave momentum flux varies between about
traditional limit wave steepness given by
5% for low amplitude, long period waves to nearly
30% for waves approaching limiting steepness.
Hlimit
0:412 tanhkh
27
To better represent the maximum depth-integrated
L
wave momentum flux in nonlinear waves, Hughes
(2004) used Fourier approximation wave theory for
which overestimates limiting steepness for long
regular steady waves over a horizontal bottom. He
waves and underestimates limiting steepness for short
determined wave kinematics and calculated values of
waves.
the dimensionless wave momentum flux parameter for
An empirical equation for estimating the wave
selected combinations of relative wave height (H/h)
momentum flux parameter for finite amplitude
and relative water depth (h/gT2). Results were plotted
steady waves was established using the calculated
as a family of curves representing constant values of
curves of constant H/h shown in Fig. 1. A nonlinear
H/h as shown on Fig. 1.
best-fit of a two parameter power curve was per-
The dashed line on Fig. 1 gives the steepness-
formed for each calculated H/h curve, and the re-
limited wave breaking criterion tabulated by Williams
sulting coefficients and exponents for each fitted
power curve were also approximated as power
approximation
curves. The resulting, purely empirical, equation
representing the curves of constant H/h shown on
x2Hlimit
a1r a2r2 a3r3
Fig. 1 is given as
co tanh
26
1 b1r b2r2
g
A1
MF
h
2
where r=x h/g, a1=0.7879, a2=2.0064, a3=0.0962,
A0
28
qgh2
gT 2
b1=3.2924, b2=0.2645 and co=1.0575. Sobey noted
max




 Previous Page
Previous Page
