1094
S.A. Hughes / Coastal Engineering 51 (2004) 10851104
4.0, 6.0 and 10.0 for a total of 100 observations. For
assumed in the derivation of Eq. (37). The root-mean-
purposes of this paper, wave height at the structure toe
squared error between measured and predicted R/h
was estimated by linear shoaling of the measured
was 0.19, excluding Granthem's 1:1 slope data.
wave height recorded at the offshore measurement
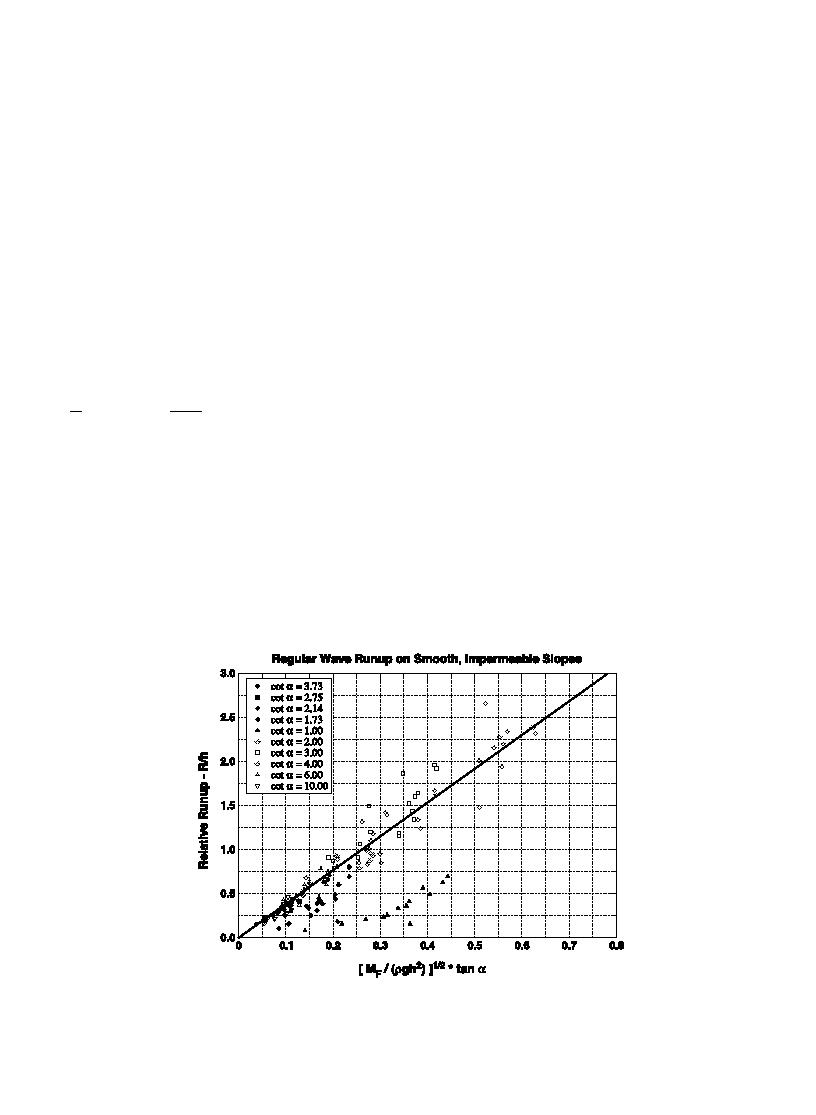
For comparison, the same data have been plotted
location. Generally, waves were significantly larger
on Fig. 4 using Hunt's Eqs. (1) and (3). (Note that the
than in Granthem's tests and only those waves with H/
ordinate axis is run-up nondimensionalized by wave
hb1.0 at the toe after shoaling were used for the
height rather than water depth.) The Iribarren number
present analysis.
characterizes run-up very well for mild slopes that
produce low no values implying plunging or spilling
The wave momentum flux parameter was estimated
for all 152 observations using the formula given by Eq.
wave breaking on the slope. As slopes get steeper and
no exceeds 2.0, scatter becomes greater. Granthem's
(28), even though application to waves with H/hz0.8
is not strictly appropriate. A best-fit of Eq. (37) to the
1:1 slope data are problematic in this plot as well.
run-up data set yielded a reasonably simple equation,
3.3. Irregular wave run-up
1=2
R
MF
3:84 tana
38
qgh2
h
Two published irregular wave laboratory data sets
were used to test the simple run-up relationship given
where (3.84 tana) represents the empirical function
by Eq. (37) for irregular wave run-up. Both data sets
CF(a) in Eq. (37). The results are shown in Fig. 3 with
represent normally incident wave run-up on smooth,
impermeable plane slopes. Fig. 5 shows irregular
the straight line representing Eq. (38). Granthem's
data are solid markers and Saville's data are hollow
breaking and nonbreaking wave run-up data for 275
markers. Most of the data follow the trend given by
values of 2% run-up elevation measured by Ahrens
the straight line with the exception of Granthem's
(1981) versus Iribarren number for steeper slopes
ranging between 1/4VtanaV1/1. The solid lines on
results for a 1:1 slope, which have much lower run-up
values than estimated. Waves on this steep slope were
(Eqs. (16) and (17)) given in the Coastal Engineering
probably surging breakers or nonbreaking waves,
Manual. Data corresponding to milder slopes are
which do not conform to the straight-line sea surface
Fig. 3. Regular wave relative run-up versus Eq. (38).




 Previous Page
Previous Page
