W. Huang et al. / Ocean Engineering 30 (2003) 22752295
2280
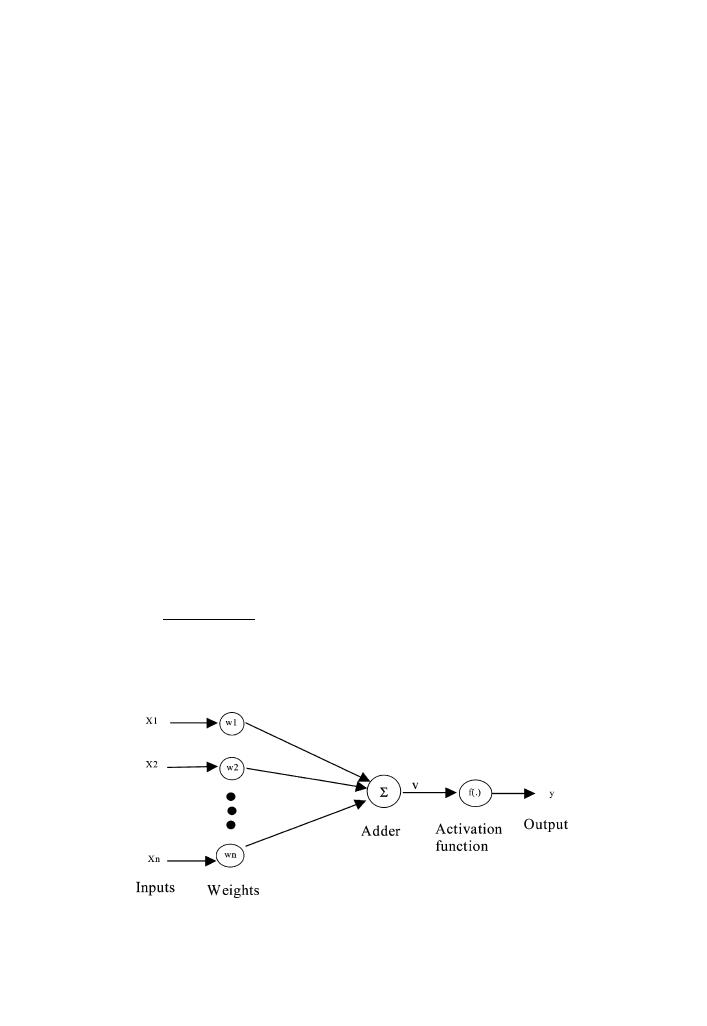
3.1. One-neuron model
By starting with a one-neuron model, it may be easier to understand the neural
network structure. A neuron is defined as an information-processing unit that is fun-
damental to the operation of a neural network. Fig. 3 shows a simple one-neuron
model to illustrate the neural network structure.
As shown in Fig. 3, there are three basic elements in an ANN:
(a) A set of connecting links, w, each of which is characterized by a weight of its
own. The weights on the connections from the input Xi (i = 1, ..., n) to the neuron
Y are wi (i = 1, ..., n).
(b) An adder, , for summing the weighted input signals; the operation constitute
a linear combiner, v:
w2x2
....
wnxn
w1x1
v
(1)
(b) An activation function, f(.), for limiting the amplitude of the output of a neuron.
The output from the neuron model can be described by
f(v)
y
(2)
There are several types of activation functions. Examples of activation functions
related to this study are given below.
i) linear function:
0
f(v)
(3)
ii) sigmoid function:
1
f(v)
(4)
exp( av)
1
where a is the slope parameter
Fig. 3.
One neuron structure.




 Previous Page
Previous Page
