W. Huang et al. / Ocean Engineering 30 (2003) 22752295
2281
iii) hyperbolic tangent function:
tanh(v)
f(v)
(5)
3.2. Multiple-layer model
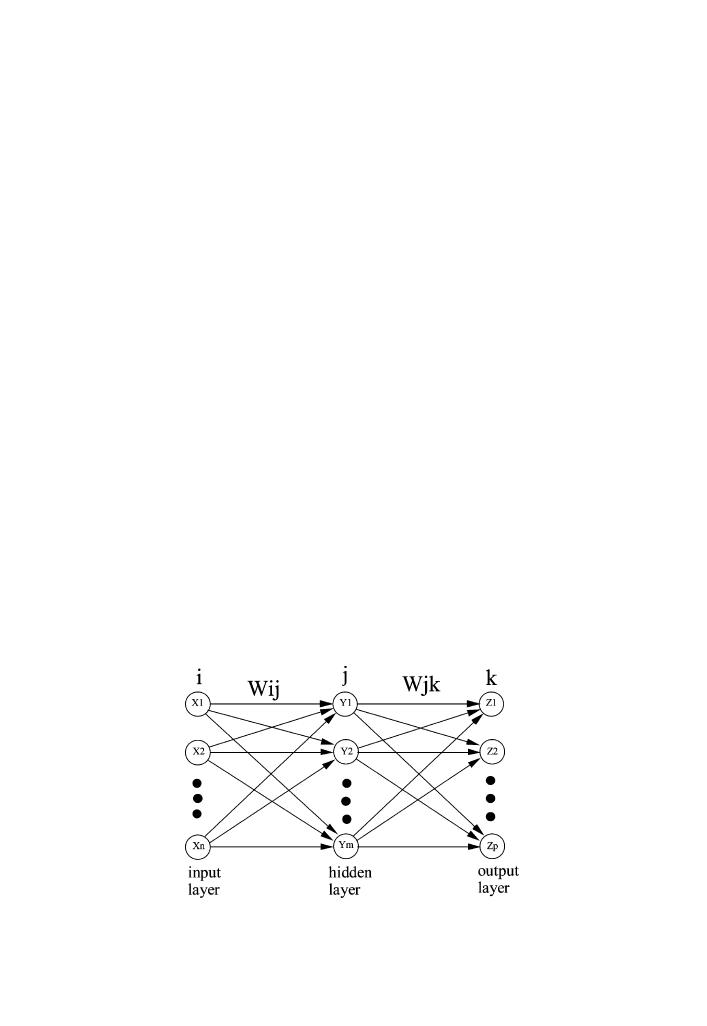
In practical applications, a neural network often consists of several neurons in
several layers. A schematic diagram of a three-layer neural network is given in Fig.
functions of wind and water levels); Yi (i = 1, ..., m) represents the outputs of neurons
in the hidden layer; and Zi (i = 1, ..., p) represents the outputs of the neural network
such as water levels and currents in and around coastal inlets. The layer that produces
the network output is called the output layer, while all other layers are called hidden
layers. The weight matrix connected to the inputs is called the input weight (Wij)
matrix, while the weight matrices coming from layer outputs are called layer
weights (Wjk).
3.3. Standard network training using gradient descent method
Multiple-layer neural networks using backpropagation training algorithms are
popular in neural network modeling (Hagan et al., 1995) because of their ability to
recognize the patterns and relationships between nonlinear signals. The term back-
propagation usually refers to the manner in which the gradients of weights are com-
puted for non-linear multi-layer networks. A neural network must be trained to deter-
mine the values of the weights that will produce the correct outputs. Mathematically,
the training process is similar to approximating a multi-variable function, g(X), by
another function of G(W,X), where X = [x1,x2,...,xn] is the input vector, and W =
[w1,w2,....wn] the coefficient or weight vector. The training task is to find the weight
Fig. 4.
A three-layer feed-forward neural network for multivariate signal processing.




 Previous Page
Previous Page
