300
L. Erikson et al. / Coastal Engineering 52 (2005) 285302
1.6
friction are consistently longer than calculated swash
durations with friction.
1.4
B10
1.2
1
6. Conclusions
0.8
Modifications were made to a model that includes
0.6
the effects of bed friction and describes shoreline
0.4
displacement as a consequence of bores collapsing at
0.2
the initial still water shoreline (SWS). Modifications
were made to account for interaction between
0
0
2
4
6
8
10
12
14
16
subsequent bores in the swash zone at and above
Time (s)
the SWS. Two mechanisms of swash interaction are
0.8
0.8
described: the first is dcatch-up and absorptionT where
0.6
0.6
the front of a wave moving landward (up-rush) is
B10
passed by a subsequent bore moving in the same
0.4
0.4
direction. The second process is dcollisionT whereby
0.2
0.2
two separate fronts collide as the back-wash of a
preceding swash lens meets the front of a subsequent
0
0
swash wave during its up-rush phase. New trajectories
-0.2
-0.2
of the shoreline are calculated when fronts collide
based on the principles of momentum for fluid
-0.4
-0.4
elements at the leading edges of the colliding swash
-0.6
-0.6
lenses. The model is a gross simplification of the true
process but does appear to at least partially grasp the
-0.8
-0.8
mechanisms involved with the interaction of subse-
-1
-1
0
2
4
6
8
10
12
14
16
quent swash waves.
Time (s)
Modifications were also made to account for the
effects that outgoing back-wash may have on incident
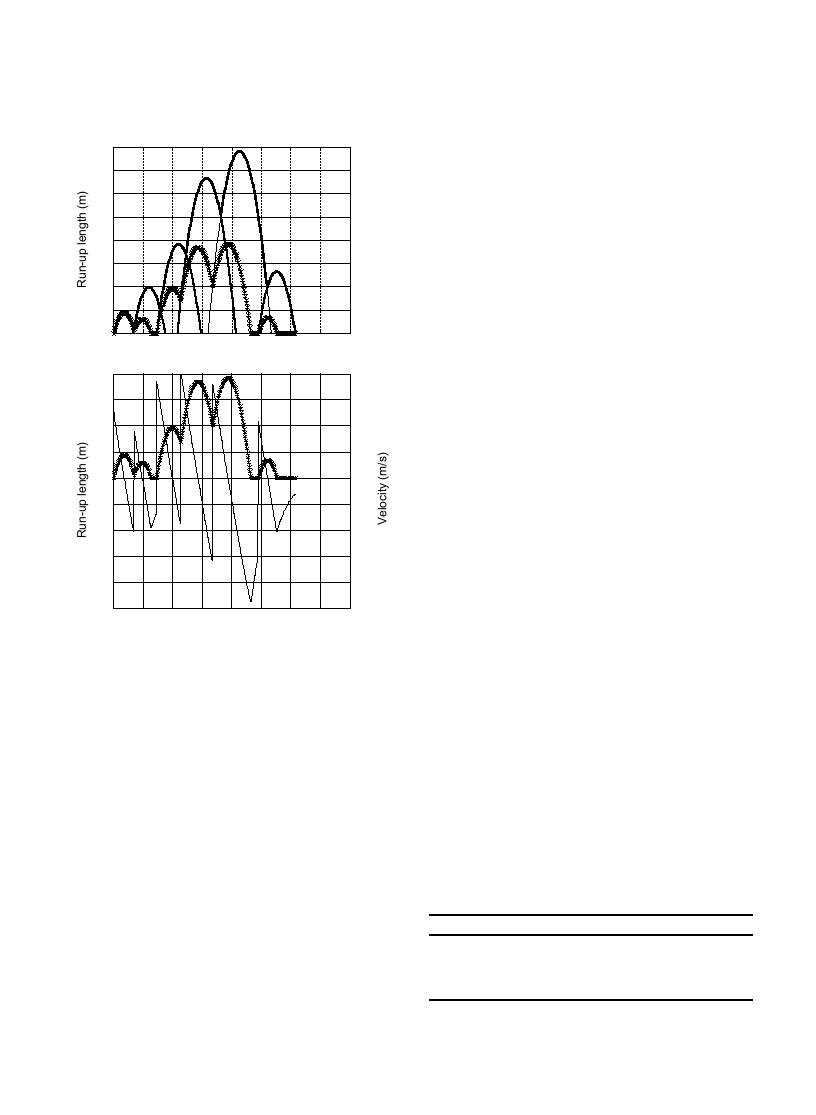
Fig. 12. Comparison of model results for case B10 with (line
bores at the SWS. This was done by imposing an
marked with 's) and without (solid line) accounting for swash
interaction.
exponentially decaying velocity of the back-wash
following its return past the SWS. Measured swash
depths at the SWS were used in the model to calculate
swash interaction. For case C1 with tanb=0.20, the
initial shoreline velocities as opposed to directly
measuring the initial up-rush velocities. Hence, any
predicted swash duration is slightly less than the
opposing velocity that the preceding back-wash may
incident wave period suggesting no interaction
have on the collapsing bore would not be accounted
between subsequent swash waves. This corroborates
for unless the wave height was decreased. Inputs to
fairly well with measured results shown in Fig. 6
where it can be seen that there is significant swash
the model were measured wave heights at the SWS
interaction for all mild slope cases and some
and their arrival times. Leading edge swash heights
interaction between the first two waves in case C1
with the steeper slope. If friction factors on the order
Table 3
of fu=0.01 and fb=0.04 were used, as suggested by
Calculated swash durations and measured incident wave periods (s)
Case
Tsu
Tsb
Ts
Tsg
T
durations would be slightly shorter but still longer
C1
0.81
0.81
1.61
1.67
1.70
than the incident wave periods. The fifth column in
B8
1.49
1.47
2.96
3.34
1.30
B9
1.64
1.65
3.29
3.60
1.30
B10
2.00
2.02
4.02
4.36
2.20




 Previous Page
Previous Page
