298
L. Erikson et al. / Coastal Engineering 52 (2005) 285302
0.6
0.6
0.5
0.5
C1
B8
0.4
0.4
0.3
0.3
0.2
0.2
0.1
0.1
0
0
0
2
4
6
8
10
12
14
16
0
2
4
6
8
10
12
14
16
Time (s)
Time (s)
0.8
0.5
0.7
B10
0.4
0.6
B9
0.5
0.3
0.4
0.2
0.3
0.2
0.1
0.1
0
0
0
2
4
6
8
10
12
14
16
0
2
4
6
8
10
12
14
16
Time (s)
Time (s)
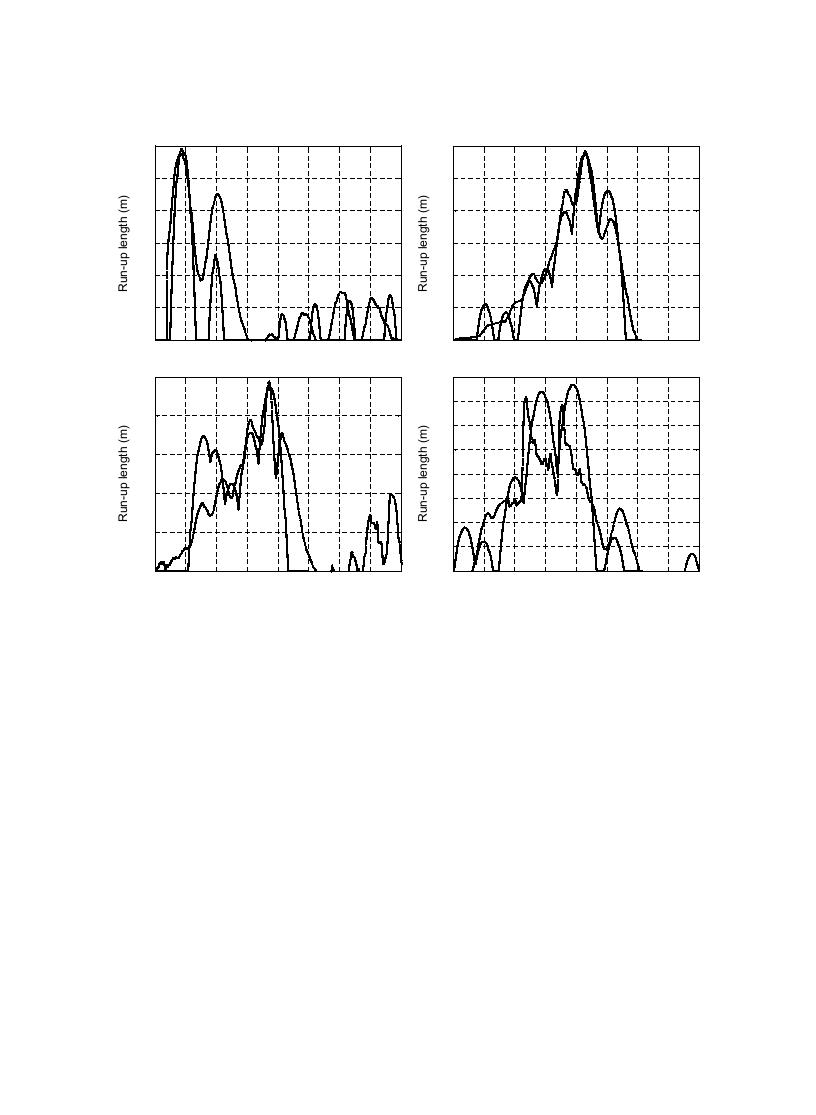
Fig. 9. Measured (dashed lines) and simulated (solid lines) run-up lengths with swash interaction. (N.B. Vertical scale differs between panels).
SWS so as to impede the initial velocity of the third
and is the predicted shoreline motion without swash
interaction (Fig. 10). The line marked with 's in
and sixth incoming bores (solid lines). The effect can
be seen in Fig. 12b showing the same predicted
shoreline trajectory with swash interaction in addition
when swash interaction is accounted for. Following
to the resulting leading edge velocity. Note the
the trajectory with swash interaction, two collisions
exponential velocity decays after the second, fifth
on the beach face above the SWS are evident: one
and sixth parabolas return to the SWS. As stated
where the back-wash of the third parabola marked
with 's intersects with the up-rush of the fourth
previously, this is a crude estimate to try to account
for interaction between outgoing back-wash and
solid-lined parabola, and another where the back-
wash of the fourth -marked parabola intersects with
incident bores, but without this adjustment, predicted
run-up lengths were consistently overestimated.
the up-rush of the fifth solid-lined parabola. Follow-
A look at Fig. 9 shows that accounting for swash
ing the collisions it can be seen how the back-wash
interaction has little effect on case C1, which has a
reverses direction to become up-rush but with limited
steeper foreshore slope (tanb=0.20) than the other
excursion length due to velocity of the back-wash
cases (tanb=0.07). The largest difference is for the
acting against the up-rush.
second wave, as this wave is affected by the
The effect of the imposed exponentially decaying
exponentially decaying velocity at the SWS of the
velocity at the SWS can be seen in the up-rush of the
first wave. In all B cases (tanb=0.07), the maximum
third and last swash-interaction parabolas. Although
run-up length is overestimated when the sequential
the back-wash has returned past the SWS, its outgoing
swash interaction is not accounted for.
velocity is assumed to decay exponentially at the




 Previous Page
Previous Page
