1098
S.A. Hughes / Coastal Engineering 51 (2004) 10851104
and thus, were excluded from the empirical
formulation as indicated by the range of applic-
ability on Eq. (40). This data set is evident on Fig. 8.
One possible explanation is that these shorter waves
on the steep 1:1 slope produced a run-up wedge with a
concave sea surface profile that was not well
approximated by the straight-line water surface
hypothesized in Fig. 2. Thus, the derived run-up Eq.
(37) is not appropriate.
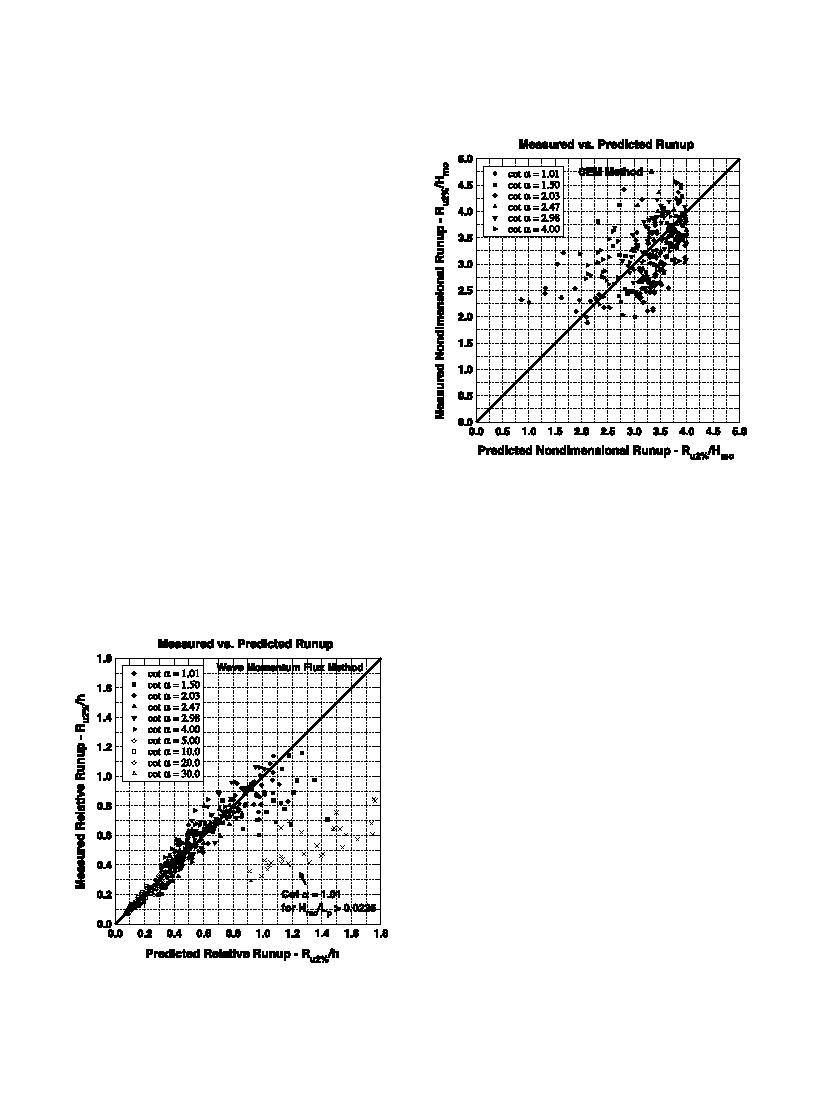
(41) to Ahrens' and Mase's observed 2% run-up
values. Mase's data are the hollow circles clustered
toward the lower left corner of the plot. With the
exception of data for slope cota=1.01 and Hmo/
LpN0.0225 (shown by the X-symbol), the prediction
is reasonable. For comparison, Fig. 10 plots Ahrens'
(1981) measurements of Ru2%/Hmo versus estimates
using the prediction equations for steeper slopes given
in the CEM (Eqs. (16) and (17)). The new irregular
Fig. 10. Comparison of Ahrens' (1981) data to predictions using
wave run-up equations exhibit less scatter for the
Eqs. (16) and (17).
Ahrens' data set then the prediction equations
recommended in the CEM.
quite mild (tana=1/30) to fairly steep (tana=2/3).
A single equation, given by either Eq. (40) or
(41), was found to work reasonably well for
Previously, separate equations based on the Iribarren
breaking waves over the entire range of slopes from
number were needed to cover this range of slopes for
breaking waves. Also note that the slope function,
F(a), in Eq. (40) or (41), i.e., (tana)0.7, has the tangent
of the slope angle raised to essentially the same power
as given by Mase (1989) in Eq. (20). As seen on Fig.
8, the 0.7 exponent of tana lessens the influence of tan
a on run-up as slope decreases. This agrees with the
observation of Douglass (1992) that slope angle
plays a less important role for wave run-up on mild
beaches.
3.4. Solitary wave run-up
Run-up of solitary waves on impermeable plane
slopes has been well studied, producing both
theoretical/empirical formulas for maximum run-
up and numerical models of the entire run-up
sequence (e.g., Synolakis, 1986; Li and Raichlen,
(2003) crafted an analytical formulation for tsu-
mani run-up, and they noted the location and
direction of maximum wave momentum flux for
the cases of initial positive and negative wave
Fig. 9. Comparison of Ahrens' (1981) and Mase's (1989) data to
forms.
predictions using Eqs. (39)(41).




 Previous Page
Previous Page
